A Basic Fan/Blower Description
Fans can be thought of as low pressure air pumps that utilize power from amotor to output a volumetric flow of air at a given pressure. A propellerconverts torque from the motor to increase static pressure across the fan rotorand to increase the kinetic energy of the air particles. The motors aretypically permanent split capacitor AC induction motors or brushless DC motors.We shall now look at this system in more detail.
Types of Fans and Blowers
Air moving devices are generally described as being either a type of fan(Fig. 1a) or a centrifugal blower (Fig. 1b). The main difference between fansand blowers is in their flow and pressure characteristics. Fans deliver air inan overall direction that is parallel to the fan blade axis and can be designedto deliver a high flow rate, but tend to work against low pressure. Blowerstend to deliver air in a direction that is perpendicular to the blower axis at arelatively low flow rate, but against high pressure.
 |
 |
| Figure 1 (a): A typical fan | Figure 1 (b): A typical blower |
There are several types of fans, some of the most common being propeller,tube axial and vane axial styles. Propeller fans are the simplest type of fan,consisting of only a motor and propeller. One problem with propeller fans isthat tip vortices are produced by the pressure differential across the airfoilsection.
A tube axial fan (the most common type in electronic cooling systems) issimilar to a propeller fan, but also has a venturi around the propeller toreduce the vortices. The vane axial fan has vanes that trail behind thepropeller in the airflow to straighten the swirling flow created as the air isaccelerated.
Centrifugal blowers may have a forward curved wheel, a backward curvedwheel, or be of the squirrel cage variety.
Basic Aerodynamics
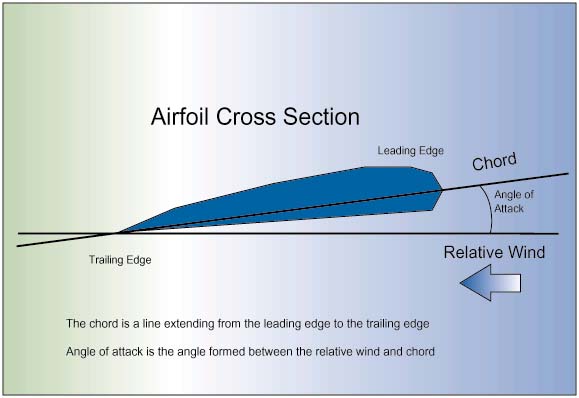
Fans are of such common use that a basic understanding of the aerodynamicsis appropriate. This understanding begins with the recognition that the bladesof a fan propeller resemble the wing of an airplane, and as such follow the sameaerodynamic laws. For example, a fan blade produces lift when the chord iselevated from the direction of the relative wind as shown in Figure 2.
Figure 2: Nomenclature for an airfoil
The elevation angle is referred to as the angle of attack (AOA). Thegreatest airflow delivery from a fan occurs when the AOA is at a minimum, butthe pressure differential across the fan is zero. As the AOA is increased, theairflow delivery decreases and the pressure differential increases. The airflowcan decrease to nearly zero, but will also deliver the maximum pressuredifferential in this condition, which is called the shut-off point. When an AOAis reached where the air will no longer flow smoothly and begins to separatefrom the blades, an “aerodynamic stall” condition exists.
Since a fan is a constant volume machine, it will move the same volumetricflow rate of air irrespective of the air density. However, the mass flow ratedoes change as the density changes. This becomes important when equipment isexpected to operate at altitudes significantly greater than sea level. Therefore the volumetric flow rate required at altitude (low density air) willbe greater than that required to achieve the same cooling as at sea level.
The Fan Curve
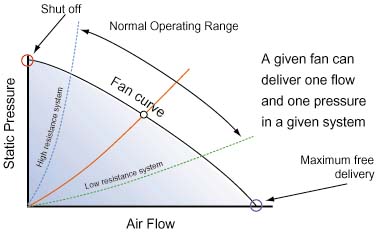
All of the aerodynamic aspects of a fan are exhibited in a fan curve such asis shown in Figure 3. The fan performance curve is one of the few curves thatare read from right to left, because you start with healthy aerodynamic flow andfollow it through to aerodynamic stall.
Figure 3: Fan/system interaction
However, in contrast to an airplane wing, there is life after stalling in afan. A stalled fan continues to deliver air, but at an increased staticpressure and a decreased volumetric flow rate, and also at the cost of anincrease in noise. If noise is not a consideration, the fan can be utilized inthis condition.
An energy viewpoint is helpful in understanding the fan performance curve.For example, at the shut-off point, the fan is in the condition of the maximumpotential energy. At free delivery, the fan is in the condition of the maximumkinetic energy. Although neither of these extreme conditions are likely tooccur in practice, they can be useful parameters in comparing fans.
The governing principle in fan selection is that any given fan can onlydeliver one flow at one pressure in a particular system. This “operatingpoint” is determined by the intersection of the fan static pressure curveand the system pressure curve. Figure 3 illustrates the operating points ofboth high and low resistance systems. It is best to select a fan that will givean operating point being toward the high flow, low pressure end of theperformance curve to maintain propeller efficiency and to avoid propeller stall. Each particular electronic packaging system should be analyzed for possiblereduction in the overall resistance to airflow. Other considerations, such asavailable space and power, noise, reliability, and operating environment shouldalso be brought to bear on fan choice.
Steps to Fan Selection
Estimate the required airflow
Before selecting a fan, obtain as accurate an estimate as possible of theheat to be dissipated, because the overall system air temperature differentialabove the inlet ambient is directly proportional to the heat dissipated. It isthen possible to estimate the amount of required cooling air. The basic heattransfer equation is:
Q· = m· Cp T
| where | |
| Q· = amount of heat transferred to system, Watts | |
| Cp = specific heat of air, J/kg·K | |
| m· = mass flow rate of air, kg/s | |
The relationship between mass flow rate and volumetric flow rate is
m· =G
| where | |
| G = volumetric flow rate, m3/s | |
The required volumetric flow rate is then calculated from
G=Q· /(Cp
T)
This yields a rough estimate of the airflow needed to dissipate a givenamount of heat at sea level. It should be noted that it is the mass flow rateof air, not its volumetric flow rate, that governs the amount of cooling.
Estimate the actual airflow
The preceding steps indicated the necessary procedure to estimate the requiredairflow in order to obtain the desired overall air temperature riseT. However, itwas also indicated that the actual operating airflow is determined bythe intersection of the fan curve and the system resistance curve. There arethree options available for estimating this operating point: (1) experimentalmeasurement using a thermal/mechanical mockup of the system, (2) calculation ofthe operating point using airflow network methods [3], or (3) calculation of thesystem airflow using computational fluid dynamics software (available fromcommercial software companies).
The experimental procedure can be used to measure the total airflow forspecific fans or several pressure-airflow data pairs can be measured to developa complete system resistance curve. The latter experimental method will thenrequire the Engineer to superimpose the selected fan pressure vs. airflow curveand system resistance curve to obtain the operating airflow.
The airflow network procedure provides adequate results when the geometry issimple and the flow path within the cabinet is known or a rough estimate can bemade. In many practical applications, however, the Designer deals with complexthree dimensional flow paths that are not known from the very first instance. In these situations, CFD software can be used. The fan performance curve can besupplied as an input to the CFD software and the software system allowed todetermine the operating point and system resistance. CFD works by numericallysolving the governing equations of flow and heat transfer in three dimensionsand takes into account the effects of turbulence and gravity. CFD can be usedto study the performance of fans in series and parallel arrangements as well asoptimize the location with respect to other objects inside the cabinet. Both ofthe computational procedures require a static pressure vs. airflow curve for thefan in question.
Irrespective of which method is chosen to estimate the system airflow, allpackaging systems are characterized by a system resistance curve of the typeshown in Figure 3. System resistance curves may usually be expressed as anon-linear expression of pressure vs. airflow:
P = K
GN
| where | |
| K = a load factor specific to the system | |
| þ = density of air | |
| G = airflow rate | |
| N = a constant which varies between 1 and 2 depending on whetherthe flow is completely laminar (N=1) or completely turbulent (N=2) |
If the estimated value of the actual airflow is significantly less than therequired value, the packaging system should be examined for regions where theairflow resistance could be reduced. Should it fail to provide an answer adifferent fan or perhaps even multiple fans should be considered. The searchfor a different fan is a simple matter of reviewing the catalogs of the variousfan vendors. The consideration of multiple fans is a little more complex.
Consider multiple fans
Combining fans in series or parallel can sometimes achieve the desiredairflow without greatly increasing the system package size or fan diameter. Parallel operation is defined as having two or more fans blowing together sideby side. The performance of two fans in parallel will increase the volume flowrate (double at maximum delivery). The best results for parallel fans areachieved in systems with low resistance. A fan curve simulating multiple,identical fans in parallel may be constructed by scaling the fan curve airflowaxis data in direct proportion to the number of fans.
In series operation, the fans are stacked one upon the other, resulting inan increase of static pressure (doubling at shut-off, but less elsewhere). Thebest results for series fans are achieved in systems with high resistance. Afan curve simulating multiple, identical fans in series, may be constructed byscaling the fan curve pressure axis data in direct proportion to the number offans.
In both series and parallel operation, particularly with multiple fans (5,6, 7, etc.), certain areas of the combined performance curve will be unstableand should be avoided. This instability is unpredictable and is a function ofthe fan and motor construction and the operating point.
It is also important to consider fan placement in the enclosure. Pressurizing the enclosure is the preferred method, since incoming air can bereadily filtered. In addition, a pressurized enclosure will prevent dustentering through cracks or crevices. The fan is also handling cooler, denserair, and it will therefore have a slightly higher pressure capability (this maybe a very slight advantage for low heat dissipating systems). An importantfeature of a pressurized system is that the fan life and reliability areincreased due to the fan ambient temperature being lower. The disadvantage ofpressurization is that heat generated by the fan is dissipated into theenclosure.
The Fan Laws
Sometimes it may be necessary to determine the output of a given fan underother conditions of speed or density, or to convert the known performance of anair mover of one size to that of another geometrically similar unit of adifferent size. The fan laws permit this.
Geometrically similar fans can be characterized by the following fourequations:
Volumetric Flowrate: G = KqND3
Mass Flow Rate: m· =Km ND3
Pressure: P = KpN2D2
Power: HP = KHPN3D5
where:
| K = constant for geometrically and dynamically similaroperation | |
| G = volumetric flow rate | m· = mass flow rate |
| N = fan speed in RPM | D = fan diameter |
| HP = power output | |
From these relationships, it is possible to calculate a fan performance at asecond condition. Table 1 is a summary of the fan law equations in a form usefulfor fan analysis.
| Constants | Variable | Fan Laws |
| Diameter (D) Density ( |
Speed (N) | G2 = G1 (N2/N1) P2= P1 (N2/N1)2 HP2= HP1 (N2/N1)3 |
| Speed (N) Density ( |
Diameter (D) | G2 = G1 (D2/D1)3 P2= P1 (D2/D1)2 HP2= HP1 (D2/D1)5 |
| Diameter (D) Speed (N) VolumetricFlow Rate (G) |
Density ( |
P2 = P1 ( HP2= HP1 ( |
| Diameter (D) MassFlow Rate (m.) |
Density ( |
G2 = G1 ( P2= P1 ( N2= N1 ( HP2= HP1 (N2/N1)2 |
Cabinet Cooling Hints
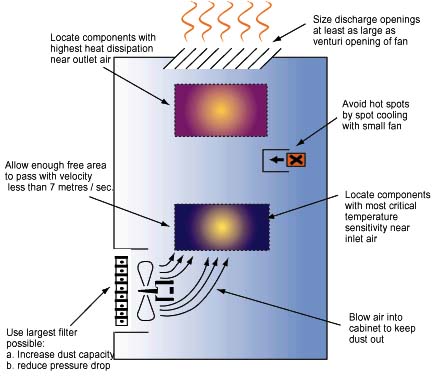
In addition to selecting a fan, there may be some choice in the location ofthe fan or fans, and in this regard, the illustration in Figure 4 may proveuseful. The following comments should also be kept in mind with regard to fanlocation:
1). Locate components with highest heat dissipation near the enclosure airexits.
2). Size the enclosure air inlet and exit vents at least as large as theventuri opening of the fan used.
3). Allow enough free area for air to pass with velocity less than 7meters/sec.
4). Avoid hot spots by spot cooling with a small fan.
5). Locate components with the most critical temperature sensitivitynearest to inlet air to provide the coolest air flow.
6). Blow air into cabinet to keep dust out, i.e. pressurize the cabinet.
7). Use the largest filter possible, in order to:
a. Increase dust capacity
b. Reduce pressure drop.
Figure 4: Cabinet Cooling Hints
References
1. Abbot, Von Doenhoff, Theory of Wing Sections, DoverPublications, New York, NY, 1959.
2. Daly, Woods Practical Guide to Fan Engineering, Woods of Colchester,Ltd, 1992. The following previous articles in Electronics Cooling are relevantto this article.
3. Ellison, Gordon, N., Fan Cooled Enclosure Analysis Using a First OrderMethod, Electronics Cooling, Vol. 1, No. 2, October 1995, pp. 16-19.
4. Woolfolk, Alan, Specifying Filters for Forced Convection Cooling,Electronics Cooling, Vol. 1, No. 2, October 1995, pp. 20-23.