John McDonald, Latigo Optics and Grant Albright EDO/Barnes Engineering Division
Introduction
Infrared imaging methods provide unequaled ease and flexibility forinvestigating micro-circuit temperatures. The researcher need only slide thecircuit under the objective lens and power it up in order to measure thetemperatures throughout the micro-circuit at once, precisely and withoutphysical contact. With the infrared instruments available today, workers canmeasure temperature differences as fine as 20 to 40 milliKelvin (equal tomilli-degrees Celsius) and see spatial features as fine as a few microns. Infrared measurements are not only accurate but also the fastest available andoffer the least disturbance to the point being measured. In terms of humanbandwidth, the amount of information conveyed is astounding. The researcherliterally gets the entire picture of how the heat is distributed over the partand how it is changing in real time. Infrared imaging has a decided advantagefor navigating under the microscope, compared to methods which require theworker to paint an obscuring liquid crystal or fluorescent material onto thecircuit.
Micro-circuits present special problems for infrared temperaturemeasurement. They use liberal amounts of metal which makes them veryreflective. This reduces their infrared emissions and contaminates theirsignature with stray emissions reflected from elsewhere in the environment. However, through consistent effort and clever application of the laws ofradiation physics, these problems have largely been solved. Practical thermalimaging microscopes are now available with point and click operation. In thisarticle, we discuss the fundamentals of infrared physics as they apply tomeasuring micro-circuit temperatures and we present example images from atypical measurement.
Planck’s Law
Every object whose temperature is not absolute zero emits thermal radiation.A fireplace poker or a light bulb filament may not be hot enough to visiblyglow, but most of the energy emitted by objects within 50 degrees C of roomtemperature is emitted within the 3 to 14 µm wavelength region. Thefundamental description of thermal radiation is the Planck blackbody radiationlaw:
| Where | |
| Q | is in photons per second per cubic centimeter and gives the thermalphotons distributed over wavelength, emitted into a hemisphere from a givensource area |
| c | is the velocity of light, 3 x 1010 cm/s |
| h | is Planck’s constant, 6.63 x 10-34 watts/s2 |
| k | Boltzmann’s constant, 1.38 x 10-23 watts s / °Kelvin |
| is the wavelength in centimeters | |
| T | is the source temperature in degrees Kelvin. |
Infrared microscopy makes use of this radiation by using detector arrays,such as Indium Antimonide and Mercury Cadmium Telluride, which are sensitive toinfrared wavelengths. These detector materials are available in the form ofcharged coupled device (CCD) arrays which are two dimensional arrays, much likethose used in video cameras. An infrared microscope is constructed byassembling such an array with appropriate infrared optics. A personal computeris added to calculate the device temperature based on the flux received by thedetector. The detector material is usually cooled to liquid nitrogentemperatures. Ordinary glass lenses are opaque in the mid to longwave infrared,so infrared microscopes as well as military thermal imagers use exotic lensmaterials such as silicon, zinc selenide, or germanium. Indeed, the number ofpractical IR lens materials is limited to just 6 or 8 which are not terriblyexpensive, toxic or soluble in water. This compares poorly with the hundreds ofoptical glasses available for visible wavelengths, which offer the infrareddesigner some advantages, such as higher indices of refraction, and it is nottoo difficult to obtain infrared optics.
The Concept of Emissivity
Planck’s law was derived for a “blackbody” – a source which bygeometry or material is perfectly efficient in absorbing radiation and is hence”black”. The blackbody does not reflect light so any radiationemanating from such a source is derived solely from the thermal properties ofthat source. Unfortunately, microcircuits are made of materials which makenotoriously poor infrared sources. To apply Planck’s law for temperaturemeasurement, we must introduce the concept of emissivity. The emissivity of a source is the ratioof its actual radiant emittance to that of a perfect blackbody at the sametemperature.
Sources which are not perfect are known as gray-bodies or selectiveemitters. A gray-body is one which emits radiation in exactly the same spectraldistribution as a blackbody at the same temperature, but with reduced intensity. A selective emitter is one in which emissivity
() varies with wavelength.
Silicon is a selective emitter but, fortunately, over a small spectralbandwidth, it behaves like a gray-body, permitting us to use classic Planckmathematics to infer its temperature, if we know its emissivity. Figure 1 showsa map of the emissivity of a typical micro-circuit. The metal layers areclearly visible and the color scale shows that the metal layers have about halfthe emissivity of the doped silicon.
What to do about Reflected Light?
When radiant energy is incident on a surface, three things can happen: afraction of the energy a may be absorbed; a fraction r may be reflected;and a fraction may betransmitted through the part. Since energy is conserved the sum of thesefractions must equal 1:
+ r+
= 1 Equation 3
Good absorbers are good emitters and empirically it turns out that amaterial’s absorbivity equals its emissivity.
=
Using this, we can restate Kirchoff’s law as:
+ r+
= 1 Equation 4
Any part which is a poor absorber or emitter will be a good reflector or agood transmitter. When examining a part with an infrared microscope, some ofthe detected radiation inevitably comes from elsewhere, either passing throughthe part or being reflected from it. This is certainly true of integratedcircuits. They are fabricated chiefly from silicon and metal which haveparticularly low emissivity.
Compensating for Low Emissivities
When emissivities are very low, the instrument is as likely to measure thetemperature of the room as it is the part being tested. What the instrumentactually measures is three blackbody functions, one for each of the emitted,reflected and transmitted component as in equation 5.
where
is theintegrated photon flux seen by the detector. The emitted radiation ischaracteristic of Ts, the source temperature, and the reflected andtransmitted components are likely to be characteristic of the ambient surroundat temperature Ta. A typical value for
may be 10% for a metallayer on a micro-circuit, so that if the part temperature and ambienttemperature are close, the instrument will detect mostly radiation from theroom. Fortunately, the flux increases approximately to the 3rd power oftemperature so the researcher can make the first term dominate by raising thetemperature of the part to be measured substantially above the room ambient. One method of accomplishing this is to mount the part on a thermoelectric stageand to elevate the base temperature to 70°C or more. This will effectivelymask any contribution from the ambient.
Pixel by Pixel Emissivity Correction
Most infrared radiometers allow no more than a single user estimate for thetarget emissivity and they employ this single input for all pixels in the image.Microcircuits have naturally low emissivity and often 2 to 1 variation inemissivity between metal layers and silicon so this could lead to seriouserrors. It is therefore more accurate to measure emissivity at each pixellocation. Since the device is mounted on an opaque substage, we can assume thatthe optical transmission of light through the device is zero.
Equation 1, when integrated over the detector’s sensitive wavelengths, canbe rewritten as:
Nm1=N1 + (1-)Na Equation 6
and again for the source at a different temperature
Nm2=N2 + (1-)Na Equation 7
| Where: | |
| Nm1 | is the radiance measured by the detector with the source at a knowntemperature. |
| is the radiance corresponding to source at a known temperature and atemissivity |
|
| (1- |
is the contribution from the room ambient. |
| N | in these cases is the photon flux integrated over the sensitivewavelengths of the detector N = |
By subtracting the two equations the ambient term drops out and solving for:
The emissivity for each pixel is the difference between the measuredradiance for each temperature divided by the difference between the calculatedradiance at each temperature for a perfect blackbody.
By fixing the part firmly to a thermo-electrically driven substage andmeasuring the radiance of the unpowered device at 2 temperatures, we cancalculate the emissivity of the circuit to a high accuracy for each pixel.
Limitations
All microscopes have a resolution limit proportional to the wavelength andinfrared microscopes utilize long wavelengths. Infrared inspection will neveroffer a resolution approaching the submicron feature size of the latestcircuits. The limit of resolution for a microscope is given by the SparrowCriteria, which is more aggressive than the better known Rayleigh Criteria.
Where:
d is the minimum separation between features to be resolved
is the wavelength oflight
N.A. is the numerical aperture of the microscope objective.
Without oil immersion, the numerical aperture is theoretically limited to 1,and practically limited to 0.95. In the semiconductor industry, long workingdistances between the objective and the integrated circuit further limits theN.A. It is convenient to assume an N.A. of 0.5 for which the Sparrow Criteriais the same as the wavelength. The Sparrow Criteria is an actual physicallimit, which is independent of magnification. Additional magnification makesthe blurred area appear larger, not less blurred. The current generation ofinfrared microscopes operates at about 5 µm wavelength, which limits thefeature resolution to about the same dimension. Research is under way todevelop instruments which operate at 2 to 3 µm, but they are not yetavailable. An application of Planck’s law for wavelengths shorter than 1 µm,suggests that there is too little thermal energy at short wavelengths to makesuch a system practical. Current state-of-the-art microthermal imagingmicroscopes operate between 1.5 to 5.5 microns wavelength with a resolution ofabout 5 microns and a sensitivity of about 100 milli-Kelvin. Within thoselimits there is a lot of information available in a microthermal image, as canbe seen in the following examples.
Examples
The following example images and the earlier emissivity image were acquiredusing the EDO Barnes’ Infrascope which is capable of resolving 5 micron featuresand has a sensitivity of about 0.1°C. Figure 2 shows a sequence of 4images. The two radiance images were taken at different substage temperaturesand used to calculate the emissivity image, also shown. The fourth image wastaken with the part powered up and it employs both the emissivity correction anda correction to remove the background ambient. The temperature image isreproduced in Figure 3. The instrument captured 5 separate images to producethis result, all automated and the result of a single mouse click. It tookapproximately 10 minutes to mount the previously delidded part, and 5 minutes toset up and capture the images.
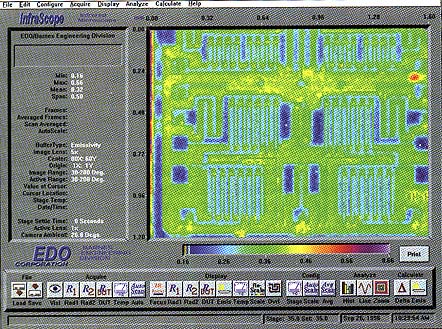
Figure 3 – Full screen image of powered uptransistors. |
(Select for a full-screen version) |
Acknowledgments
Thanks to EDO Barnes Engineering Division, Shelton CT, for the use of theirInfrascope to make these images.
References
1. Levine, M.A., Solid State Cooling with Thermoelectrics,Electronic Packaging & Production, Nov. 1989.
2. Melcor Corporation, Thermoelectric Handbook, Sept., 1995.
3. Rowe, D. M., CRC Handbook of Thermoelectrics, CRC Press, Inc., 1995.
4. Smythe, Robert, Thermoelectric coolers take the heat out of today s hotchips, Electronic Products, Aug. 1995.
For Additional Information
1. Richard D. Hudson, Jr., Infrared System Engineering, Wiley, 1969, ISBN 471418501.
2. Warren J. Smith, Modern Optical Engineering, McGraw-Hill,1990 ISBN 0-07-059174










