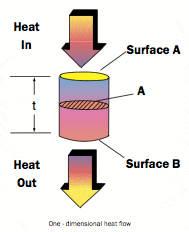
The simplest heat flow situation is that described as “one-dimensional heat flow”. The Figure illustrates a one-dimensional heat flow situation. It shows heat flowing in one face of an object and out the opposite face. Each face is at a uniform temperature. There is no heat flow out of the sides of the object. The cross- sectional area of the object in the direction of heat flow is constant. This is called one-dimensional heat flow, because the temperature in the object is a function of only one dimension – the distance from either face of the object.
If TAB is the temperature difference between the two faces and Q is the heat flowing into or out of the object per second, the relationship between these two quantities is described by the following equation:
where A is the cross-sectional area of the object, is its thermal conductivity, and t is its thickness. The predictions of this equation are consistent with our intuition: increasing A, , or TAB, or decreasing t, will increase the heat flow.
If one assumes that the thermal conductivity is independent of temperature, then one can calculate the thermal resistance for heat to flow through the object along the indicated path between surfaces A and B. This thermal resistance, AB is calculated from the following equation:
The thermal resistance is a handy figure of the efficiency of heat transfer for one component compared with that of another. The reader should note that, consistent with intuition, decreasing the thickness or increasing the cross-sectional area or thermal conductivity of an object will decrease its thermal resistance.