In last issue’s column, we discussed heat loss by convection and radiation from a printed circuit board in which heat spreads in a 2-D pattern. Here, we look at a slightly simpler situation, namely that of heat transfer by a fin into the ambient air. The situation is illustrated in Figure 1, where, for simplicity, the heat is shown flowing only out of the top surface of the fin. Two heat transfer processes are depicted: conduction along the length of the fin and the extraction of heat into the air by convection and radiation.
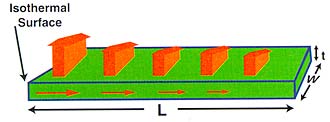
The vertical surface on the left side of the fin is assumed to be at a constant temperature. In practice, it would be attached to a component containing a heat source. The thermal resistance for heat to flow from the isothermal surface into the air by way of both the top and bottom surfaces of the fin is given by the following equation:
where 
= (2h/
t)1/2, the dimensions L, t, and W are defined in the Figure, is the thermal conductivity of the fin material, and h is the heat transfer coefficient. The graph illustrates the effect of the conductivity of the fin on 
FIN-AIR at three different values of h for a fin with the following dimensions: W = 25 mm, L = 50 mm, and t = 1.57 mm.
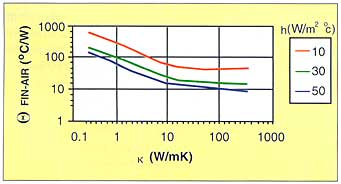
One notices that for a fin of the dimensions indicated, increasing the conductivity significantly afftects FIN-AIR until exceeds 100 W/mK. At that point the contribution of the conduction thermal resistance of the fin becomes small (the fin becomes nearly isothermal) and the limiting factor is the thermal resistance for heat to flow from the surface to air. (Refer to Calculation Corner, January, 1998, for further information on calculating and using h.) A well-designed fin will be of such a conductivity and dimensions that the conduction losses in the fin would be small to maximize the heat transfer into the air.
The above equation can be used to calculate the thermal resistance to air for one quadrant of a single-layer JEDEC-standard thermal test board. The trace region of such a board would have an effective thermal conductivity of about 10 W/mK. The value for W used would be the distance spanning the traces to which the package is actually attached. Here, as before, W is assumed to be 25 mm. The thermal resistance to air is in the range of 30 -75°C/W. (One divides these values by 4 to get the thermal resistance of all four quadrants in parallel.)
