Because the accurate determination of thermal conductivity is a demanding task (often not recognized by either designers or vendors), methods, based on the measurement of another physical property that is uniquely coupled to thermal conductivity, are very challenging.
One such method is based on the so-called Wiedemann-Franz Law, which links the thermal conductivity to the electrical conductivity according to:
k/ 
= L�T
where k is the thermal conductivity in W/mK, T is the absolute temperature in K, is the electrical conductivity in 
-1m-1, and L is the Lorenz number, equal to 2.45 10-8 W/K2.
Clearly there is a world of difference between the measurement of electrical conductivity and that of thermal conductivity. The relationship holds only for materials with more or less freely moving electrons; in other words, metals (at least at room temperature). The Wiedemann-Franz Law is based on arguments derived from the kinetic theory of gases applied to solid-state physics, and was formulated some 150 years ago.
The free electrons in the metal lattice interact with the lattice vibrations (called ‘phonons’) thereby picking up energy. When an electric field is applied, the electrons carry this energy and hence they transport both an electrical charge and heat. Obviously a direct relationship should exist.
However, phonons also transport heat (it is the only transport mechanism in insulators). Only in those cases where the electron contribution is much higher than the phonon contribution does the Wiedemann-Franz Law hold reasonably well. This happens to be the case for all pure metals, but the Law breaks down for semiconductors (and maybe also for some alloys).
In this century the theory has been improved through quantum mechanics, and it is interesting to observe that both theories generate about the same value for the Lorenz number. However, this is purely coincidental. Two terms in the kinetic gas formulation appeared to be way off the right value, but, as it happened, they cancel each other.
 |
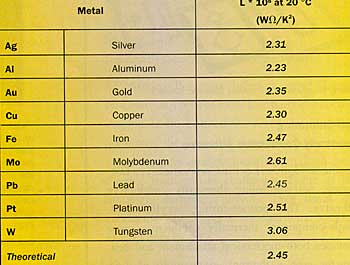Source: Physical Property Data for the Design Engineer, ed. Beaton & Hewitt, Hemisphere, 1989
The table above provides experimental values for L for a number of pure metals.
Except for Tungsten, the correspondence with the theoretical value is rather good; certainly for practical applications. I don’t know if data are available for other electron-conductors of practical interest, such as alloys and the hydrides, nitrides and carbides of transition metals like Tungsten and Titanium, and I would appreciate any comments by readers pointing towards additional data.
