don’t underestimate radiation in electronics cooling
Bruce M. Guenin, Ph.D., Associate Editor, Amkor Technology, Inc.
It is easy to underestimate the role of thermal radiation as a significant contributor to electronics cooling in environments without forced air flow. By its very nature it is invisible. The proper
treatment of it can be intimidating due to the complicated nature of the phenomenon in environments in which localized hot regions are in the view of other localized hot regions.
However, it is possible to get a basic understanding of radiation without even worrying about such complications as view factors.The first thing to do is to respond to the basic engineering urge to
linearize anything possible. Hence, Equation 1 is a recasting of the familiar Stephan-Boltzman equation, dividing it by the temperature difference between a surface (assumed isothermal) and the facing surface
(assumed to be at the air temperature). The result is a heat transfer coefficient, which represents the effect of radiation at a given temperature.
The numerical factor is the Stephan-Boltzmann constant and is the emissivity. The emissivity is in
the range 0.8 – 0.9 for dielectrics and 0.1 – 0.2 for commercial metals. The temperatures are expressed in absolute temperature Kelvin units.
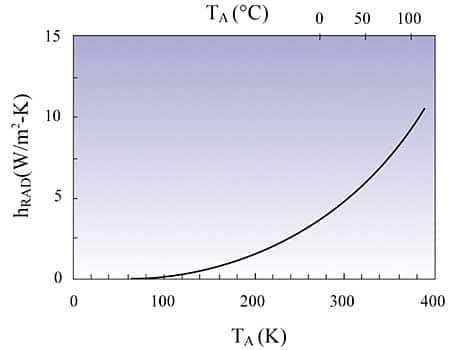 |
Figure 1. Temperature dependence.
Even though we have linearized the S-B equation, the resultant heat transfer coefficient is still highly
temperature-dependent. In fact, it is proportional to the third power of the absolute temperature. Figure 1 illustrates this temperature dependence, where we have assumed an emissivity of 0.8 and a
temperature difference between the surface and the air of 1°C.
The lower x axis indicates absolute temperature.The upper x axis indicates degrees centigrade in the
range of interest to electronics cooling. At a typical ambient temperature range, say around 50°C, hRAD is approximately 6 W/m2-K.
It is useful to compare the radiation heat transfer coefficient to the heat transfer coefficient applicable
to a horizontal printed circuit board in a large enclosure. This expression represents an average for heat transfer from the top and bottom surfaces of the board [1].
The following graph, Figure 2, compares the magnitude of the radiation and natural convection heat transfer coefficients as a function of the temperature difference between the surface and air
temperature, where the air temperature is assumed to be 50°C.
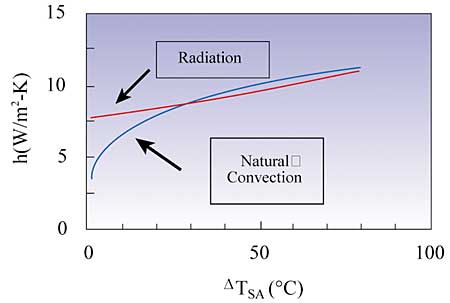 |
Figure 2. Magnitude of radiation and natural convection heat transfer coefficients.
One sees that the hRAD is actually greater than hNC up to a temperature difference of about 25°C. For temperature differences exceeding this, they are nearly equal.
In more realistic situations, the details of radiation heat transfer can be very complicated. The relative
heat transfer by radiation and natural convection can differ significantly from that demonstrated in this comparatively simple example. However, the fact remains that radiation heat transfer is significant in
many natural convection cooling situations and must not be overlooked.
Reference
1 B. S. Lall, B. M. Guenin, R. C. Marrs, and R. J. Molnar, “Parametric FEA Thermal Model for
QFP Packages,” Proceedings, SEMI-THERM XII Conference, March, 1996, pp. 105-110.




