Heat Transfer Enhancement By Using Nanofluids For Cooling Of High Heat Output Microprocessor

It is well known that the thermal properties of heating or cooling fluids play a major role in the development of energy-efficient heat transfer equipment. However, conventional heat transfer fluids such as water, ethylene glycol and engine oils have, in general, poorer heat transfer properties than most solids. In spite of considerable research efforts, major improvements in heat transfer capabilities, especially for cooling of high-heat-output electronic devices, have been lacking [1]. As a result, a clear need exists today to develop new strategies to improve the effective heat transfer behaviors of conventional fluids.

Recent developments in nanotechnology have created a new and rather special class of fluids, called ‘nanofluids’, which appear to have great potential for cooling applications [2]. The term nanofluid refers to a two-phase mixture in which the continuous phase is usually a liquid and the dispersed phase is composed of extremely fine metallic nanoparticles, usually less than 50 nm in size. Some current nanoparticle dispersions of engineering interest are actually manufactured and commercially available [3]. It has been shown that the thermal properties of such a mixture appear signifcantly higher than those of the base fluid.

In fact, some experimental data have revealed that even for a relatively low particle loading (e.g., 1 to 5% in volume), the effective thermal conductivity of the mixture can be increased by almost 20% compared to that of the base fluid [4]. Recent experimental work [5] and numerical investigations [6, 7] have confirmed the heat transfer enhancement of nanofluids in some confined flow situations. Such an enhancement can be attributed, in part, to the corresponding enhancement of the nanofluid thermal properties (with respect to those of the base fluid).

On the other hand, due to the random movement of nanoparticles, another interesting phenomenon, called ‘thermal dispersion’, takes place within the mixture. Such thermal dispersion is believed to play an active role in the increase of energy exchange rates in the fluid [8]. Furthermore, due to the nanometer size of particles, some fascinating yet rather complex phenomena exist at the liquid-solid particle interface, such as the intermolecular energy exchange, the liquid layering on this interface, as well as the heat transport within the particles themselves (phonon effects). To date, these phenomena are still not very well understood and are under intensive investigation from researchers around the world [9]. Nanofluids appear a very interesting alternative for heat transfer applications, in particular for electronics cooling and micro-heat transfer [2, 10].

In the present work, we have attempted to determine the beneficial effects due the use of such nanofluids in cooling of electronic devices. The problem consists of the developing laminar forced flow of a nanofluid flowing inside a heat sink that is installed on top of a high heat output microprocessor. The heat sink considered is of a rectangular slot type measuring 50 X 50 X 10 mm with a 3 X 48 mm fluid flow cross-section (Figure 1). The flow is steady and laminar, and the fluid has uniform axial velocity and temperature profiles at the inlet. On the heat sink external surfaces, the convective condition of heat loss towards the ambient air has been imposed throughout, except for a 10 X 10 mm contact area where the total heat, Q, has been specified.

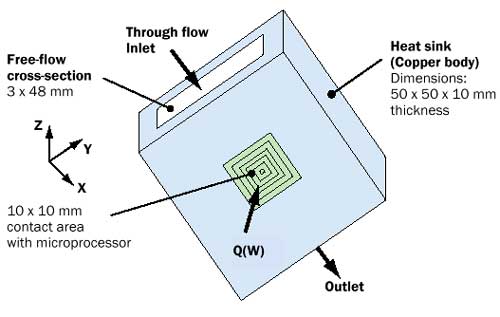Figure 1. Geometrical configuration of the slot-type heat sink considered.Among the dimensionless governing parameters, one must cite the flow Reynolds number (Re=V₀D_h/�), the Prandtl number (Pr=C_p�/k), and the particle volume concentration, , where V₀ is the fluid inlet velocity, D_h is the cross-section hydraulic diameter, C_p, , �, and k are, respectively, specific heat, density, dynamic viscosity, and thermal conductivity of the nanofluid. All properties are evaluated at the fluid inlet temperature, T0 [6]. The system of governing equations was successfully solved by using the control-volume-based method [11] and the staggered non-uniform grid.

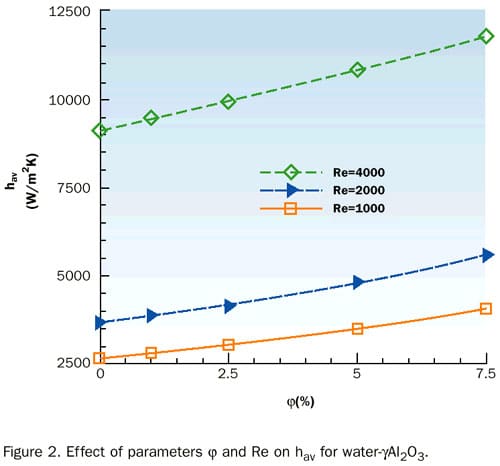The numerical results predict that the inclusion of nanoparticles within the base liquid has produced a noticeable effect on the heat sink cooling performance. It has been found that the maximum junction temperature, T_max, decreased with an increase of the parameter, . For example for the case Re=2000, Q =150W, and using a water-Al₂O₃ suspension, T_max has decreased from 65.8° to nearly 58.4°C for , increasing from 0 to 7.5% (Table 1). The corresponding increase of the averaged heat transfer coefficient, h_av, was evaluated to be 53% (Figure 2).Table 1. Effect of parameters and Re on T_max (Q=150W).

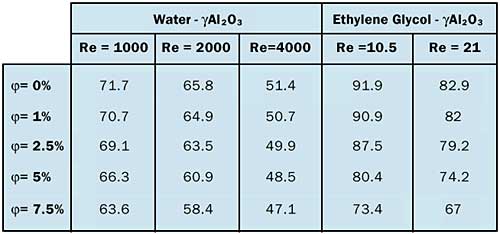Also, as one can expect, increasing the mass flow rate (or the Reynolds number) would considerably enhance the cooling rate. Thus, for example, for =5%, T_max has decreased from 60.9° to 48.5°C for Re, increasing from 2000 to 4000, which corresponds to an augmentation of nearly 125% of h_av. Similar heat transfer enhancement has also been obtained using an ethylene glycol-Al₂O₃ suspension. The authors are presently undertaking further numerical studies to compare heat transfer enhancement as given by different internal geometries of the heat sink. We have also planned some experimental work in the near future to carry out a close assessment of the above numerical results.The authors wish to thank the Natural Sciences and Engineering Research Council of Canada for financial support to the present project.

References

1. Azar, K., “Cooling Technology Options, Parts 1 & 2”, ElectronicsCooling, Vol. 9, No. 3, pp. 10-14, and Vol. 9, No. 4, pp. 30-36, 2003.
2. Lee, S., Choi, S.U.-S., “Application of Metallic Nanoparticle Suspensions in advanced Cooling Systems”, ASME Publications PVP-Vol. 342/MD-Vol. 72, pp. 227-234, 1996.
3. Nanophase Technologies, Romeoville, IL, USA, http://www.nanophase.com
4. Wang, X. et al., “Thermal Conductivity of Nanoparticles-Fluid Mixture”, Journal of Thermophysics and Heat Transfer, Vol. 13, No. 4, pp. 474-480, 1999.
5. Pak, B. C., Cho, Y. I., “Hydrodynamic and Heat Transfer Study of Dispersed Fluids with Submicron Metallic Oxide Particles”, Experimental Heat Transfer, Vol. 11, No. 2, pp. 151-170, 1998.
6. Ma�ga, S.E.B. et al., “Heat Transfer Behaviors of Nanofluids in Uniformly Heated Tube”, Superlattices and Microstructures, Vol. 35, No. 3-6, pp. 543-557, 2004.
7. Roy, G., Nguyen, C.T., Lajoie, P.-R., “Numerical Investigation of Laminar Flow and Heat Transfer in a Radial Flow Cooling System with the Use of Nanofluids”, Superlattices and Microstructures, Vol. 35, No. 3-6, pp. 497-511, 2004.
8. Xuan, Y., Roetzel, W., “Conception for Heat Transfer Correlation of Nanofluids” International Journal of Heat Mass Transfer, Vol. 43, pp. 3701-3707, 2000.
9. Keblinski, P. et al., “Mechanisms of Heat Flow in Suspensions of Nano-Sized Particles (Nanofluids)”, International Journal of Heat Mass Transfer, Vol. 45, pp. 855-863, 2002.
10. Goodson, K. et al., ElectronicsCooling, Vol. 8, No. 4, Technical Brief, pp. 46-47, 2002.
11. Fluent 6 User’s Guide, Fluent Inc., NH, USA, 2002.