Moisture permeation in electronics

Environmental control for electronic packages and enclosures often involves understanding and managing moisture concentration. Excessive moisture combined with processing temperatures can cause damage. High humidity levels have other potentially harmful effects such as corrosion. Since the movement of heat and moisture are similar (i.e., diffusive), thermal engineers may be asked to apply their expertise to this topic. The goal of this article is to provide an overview of moisture permeation and to provide some guidance for thermal engineers. Water movement across an enclosure boundary can occur from both leakage and diffusion. If leakage is present, it is most likely the dominant transfer mechanism but for well-sealed systems, moisture diffusion through the boundary materials is relevant. The similarity of Fick’s diffusion equation (1) to the heat equation (2) gives an opportunity to use standard thermal tools to solve moisture concentration problems.

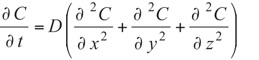(1)

C = Concentration, D = Moisture Diffusivity

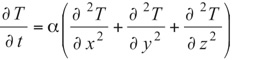(2)

T = Temperature, a = Thermal Diffusivity

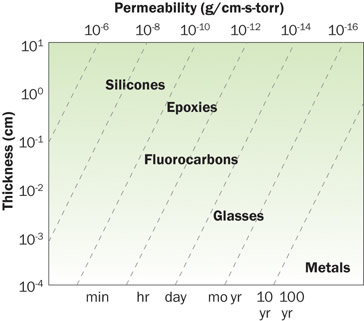
However, applying thermal tools for computing concentration is not entirely straightforward. While temperature is continuous across material boundaries, moisture concentration may be discontinuous across material boundaries. One approach for using thermal modeling tools with multiple materials is to normalize the concentration of moisture in each material by its saturation concentration and then treat the normalized fraction of concentration as the unknown variable and force continuity at the boundaries [1]. Continuing with the moisture-thermal analogy, the effective conductivity for each material becomes the moisture diffusivity times the saturation concentration. While detailed numerical analysis of moisture concentration gradients is possible (and substantially more complicated than is possible to discuss in a technical brief article), a frequent concern is simply to determine the rate of moisture permeation through a material given a vapor pressure difference on different sides of the material. This is similar to considering a net heat flow through a material with air on both sides and relating the heat flow to the air temperature difference (without a distinction between the convective and conductive components).The reader is reminded that it is the water vapor pressure difference that matters for diffusion. Maintaining a positive total pressure (but dry) condition inside of an enclosure will not prevent moisture from diffusing in when the outside air contains a water vapor partial pressure higher than the inside of the enclosure. The permeability of materials to moisture varies many orders of magnitude as shown in Figure 1. The upper horizontal scale lists the permeability while the lower horizontal axis lists the approximate time scale for permeation. The diagonal lines show the effect of thickness as shown on the left axis. The low permeability of metals and glasses are the reason they are used as materials of choice for containers that need to stay near hermetic for long time frames.
Figure 1. Range of permeability for materials [2]Several engineering disciplines have an interest in understanding and predicting moisture permeation, notably the food and building material industries, and have published substantial data. Unfortunately, much of this data is in various and often confusing forms and may not adequately describe the test conditions necessary for accurate representation of the data. ASTM E 96 recommends that measurements of permeance (g/cm²-hr-Pa) and permeability (g/cmhr- Pa) be both reported [3]. Note that the permeability as defined by ASTM E 96 (PE₉₆) is expressed in terms of measurable quantities as shown in equation 3 and is an intensive material property. Accurate measurement of PE₉₆ requires resolving small mass changes and can take a long time. For materials with very low permeation values, uncertainties in mass measurements caused by repeatability and buoyancy effects can be particularly difficult to minimize.

(3)

A frequent form of data found in literature is in terms of a transfer rate (WVTR for water vapor transfer rate or MVTR for moisture vapor transfer rate). Usual units for WVTR are (g/m²-hr) but are sometimes found with a thickness term in the numerator (gmm/ m²-hr), which can give some indication of the material thickness used in the test. Most likely, this data will not be found in SI units but in some combination of days, area, and possibly even a volumetric gas quantity at standard temperature and pressure. For this data to be useful, the test conditions must be reported.

Note that PE₉₆ for a material is equivalent to the diffusivity times the solubility and is further equivalent to the diffusivity times the Henry’s law constant when the moisture concentration is relatively small. Relatively small means that the moisture concentration in the material will respond linearly to the water vapor partial pressure in contact with the material. In this form, it is convenient to express the solubility and Henry’s law constant in mass of water per volume of material because many materials tested are not homogenous and expressing these terms with moles is difficult without a well defined molar mass. Because the solubility of many materials is dependent on temperature and concentration, it is crucial to know the test conditions that were used to generate the permeance or water vapor transport data. This would be similar to needing to measure thermal conductivity as a function of both heat flow and temperature.

As mentioned, permeation data can be found with a variety of units. For example, the building industry often reports moisture permeance in units of perms. A perm is defined as one grain of water passing through one square foot in one hour under the action of a vapor pressure differential of one inch of mercury. The corresponding unit of permeability is the perm-inch. Besides the difficulty in manipulating units, the electronics-cooling engineer is often at a disadvantage because of the need to use data out of the realm of where it was tested and the test conditions are not well documented.

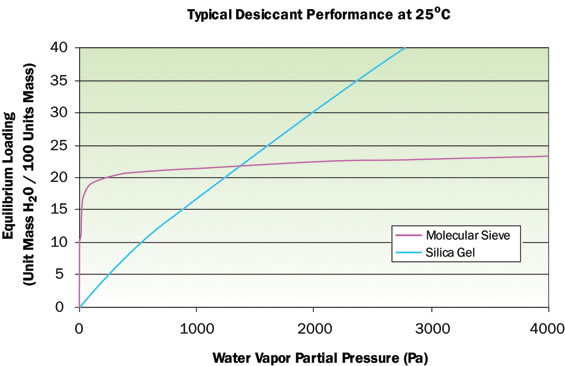
After estimating the moisture permeation characteristics of an enclosure, moisture control methods are usually considered [4]. One method of managing infiltrated moisture is with the use of desiccants. Figure 2 illustrates typical desiccant performance curves of loading versus water vapor pressure. Silica gel is found in many packaging applications and is best suited for moderate humidity levels. Molecular sieve desiccants are preferred for packages where a very low humidity level is needed. Dynamic simulation of a package with internal desiccant and varying environments is difficult to perform with thermal tools and the interested reader is referred to [5] for more information.

Figure 2. Typical desiccant performance curves

As a final comment, one reason for the variability in the literature data for moisture permeation is that, unlike heat flow, it is difficult to reduce the moisture flow properties for a material to a single coefficient that is widely applicable. Similar to thin film thermal property variations, moisture permeation in thin films is also geometry dependent and is further complicated by the fact that defects contribute to the overall measured permeation [6].

References

1. Wong, E. H., Koh, S. W., Lee, K. H., Lim, K.-M., Lim, T. B.; Mai, Y., “Advances in Vapor Pressure Modeling for Electronic Packaging,” IEEE Transactions on Advanced Packaging, Vol. 29, pp. 751-759, November 2006.
2. http://www.devicelink.com/mddi/archive/00/01/015.html
3. ASTM E96/E96M-05 Standard Test Methods for Water Vapor Transmission of Materials, ASTM International, www.astm.org
4. Tencer, M. and Moss, J., “Humidity Management of Outdoor Electronic Equipment: Methods, Pitfalls, and Recommendations,” IEEE Transactions on Components and Packaging Technologies, Vol. 25, pp. 66-72, March 2002.
5. Myers, D., “Humidity Control Simulation for Electronics Packaging,” Proceedings of IPACK03, Paper # 35057, 2003.
6. Graff, G., Willford, R., and Burrows, P., “Mechanisms of Vapor Permeation through Multilayer Barrier Films: Lag Time Versus Equilibrium Permeation,” Journal of Applied Physics, Vol. 96, No 4., pp. 1840-1849, August 2004.