A Simple Method to Estimate the Physical Characteristics of a Thermoelectric Cooler from Vendor Datasheets

Introduction

A thermoelectric cooler (TEC) is a solid-state refrigerator that operates on the Peltier effect. The absence of moving parts, compact size, precise temperature control ability and reliability all combine to make the TEC a unique refrigerator. TECs find application [1, 2] in many fields from simple food and beverage coolers for an afternoon picnic to extremely sophisticated temperature control systems in space vehicles. More and more TECs are being used to solve severe cooling problems, especially in the electronics industry; for example, the cooling of laser diodes [3].

Due to high demand and economic values, many manufacturers are marketing a wide variety of TECs [4]. Every manufacturer specifies their TECs using performance curves and several limit values: ΔT_max, I_max, V_max and Q_max [5]. Thermal management engineers need to find the highest performance TEC, optimize the operating parameters using simple calculations, and simulate the overall cooling system (including the TEC) using commercially available CFD software. To do all this it is necessary to know the basic physical properties (s, ρ and k) of the TEC materials. Unfortunately, most manufacturers do not provide this kind of information in their product catalog. Therefore, thermal designers usually find it difficult to obtain these physical properties. Huang et al. [6] designed an experiment which can accurately measure the physical properties of a TEC module. The problem is that most thermal designers usually do not have either accessibility to the necessary apparatus or sufficient time to make the required measurements.

This article presents a simple method to calculate the physical characteristics of a TEC module (i.e., device Seebeck voltage S_M, device electrical resistance R_M and device thermal conductance K_M) based upon the information ( ΔT_max, I_max, V_max and Q_max) readily available in the vendor datasheet. The fundamental physical properties s, ρ and k can then be calculated if N (number of couples) and G (ratio of the cross-sectional area/length of each thermoelectric element) are known. Further, this article presents an application example to evaluate and optimize the operating parameters of TEC by simple calculations.

Modeling

Basic Model for TEC

The following theoretical equations (1-4) for a TEC are provided in many handbooks and papers [7-10]:

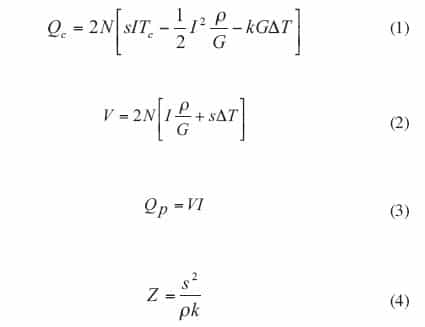To simplify, define S_M, R_M and K_M by equation (5-7):

S_M = 2sN (5)

R_M = 2ρN/G (6)

K_M = 2NkG (7)

Then, equations (1, 2 and 4) can be expressed as equations (8-10):

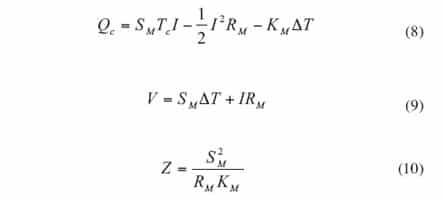The parameters s, ρ and k are fundamental physical properties of the TEC materials and S_M, R_M and K_M are the physical characteristics of the TEC as a device. The figure-of-merit, Z, is directly related with the ability of a TEC to pump heat and is a criterion to evaluate the quality of the TEC [11]. All these parameters are necessary constants in calculations or simulations using the above equations. Unfortunately, none of these are generally listed in the manufacturer’s catalogue. What the manufacturers usually list are ΔT_max, I_max, V_max, and Q_max at a specified hot side temperature T_h.

Expressions for ΔT_max, V_max, I_max and Q_max

Inspection of equation (8), reveals that DT varies as the square of current I when Q_c is zero, as shown by equation (11).

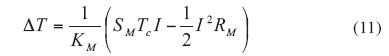Differentiating equation (11) with respect to I leads to equation (12):

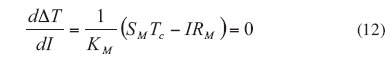Setting equation (12) equal to zero and solving for I to maximize ΔT leads to equation (13):

Equation (13) is the prerequisite to produce the maximum temperature difference ΔT_max, and the current is defined as the maximum current I_max. The voltage at this time is defined as the maximum voltage V_max. Now, inserting the value of I_max from equation (13) into equation (11) results in equation (14) for ΔT_max:

Replacing ΔT and I with ΔT_max and I_max in equation (9), an expression for V_max can be obtained, as shown by equation (15).

Usually performance specifications for a TEC lists ΔT_max, I_max , V_max at a specific hot side temperature T_h. Replacing T_c with (T_h– ΔT_max) in equations (13) and (14), equations (16) and equation (17) are obtained.

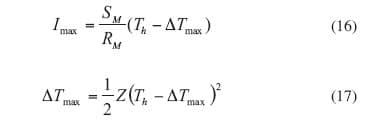In addition, Q_max occurs also at a specific hot side temperature when I = I_max and ΔT = 0�C. Therefore equation (8) can be reformed as equation (18):

Method I to Calculate S_M, K_M and R_M

Although the three TEC physical characteristics parameters S_M, R_M and K_M are unknown, as noted earlier, vendor datasheets usually give the four maximum parameters ΔT_max, V_max, I_max and Q_max, and in addition there are four equations (15-18). Any three of the four equations can be used to solve and get expressions for S_M, R_M and K_M. Method I in this article uses only three equations ΔT_max, V_max and I_max, and leaves the fourth for Q_max alone. In this way, equations (19-22) are obtained from equations (10), (15-17) to determine Z, S_M, K_M , and R_M:

As long as S_M, R_M and K_M are known, s, ρ and k can be calculated according to equations 5-7, if N and G are known.

Method II to Calculate S_M, K_M and R_M

As indicated above, any three of the four equations (15-18) can be used to solve and get the expression for S_M, R_M and K_M. Method II in this article can be used to calculate S_M, R_M and K_M according to the three equations for ΔT_max, I_max and Q_max, without using V_max. According to method II, the resulting formulations are equation (19) and equations (23-25).

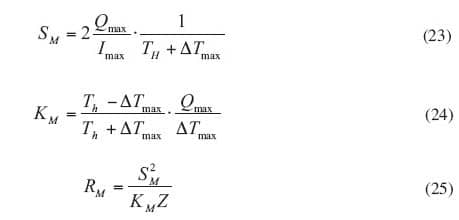Ideally, there should be internal consistency between the four equations (15-18), and the calculation results of the two methods should be the same. However, this is not always the case. Errors do exist, which can be seen in the following application example.

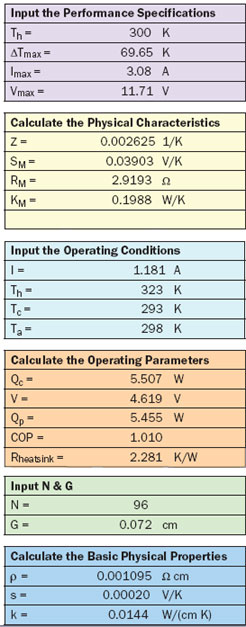
Table 1. Spreadsheet Calculator for TEC

Application and Discussions

Using the preceding formulas, a spreadsheet calculator can be made to determine the physical characteristics, basic physical properties and operating parameters of TECs as shown by Table 1. After inputting the performance specifications in terms of T_h, ΔT_max, I_max and V_max, the physical characteristics S_M, R_M, K_M and Z are calculated according to equations 19-22 in method I. Then, inputting the operating conditions I, T_h, T_c, and T_a, operating parameters Q_c, V, Q_p, COP and R_heatsink are calculated according to equations 1-3, 26 and 27.

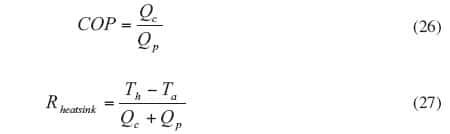In addition, if values for N and G for the TEC under consideration are provided as input, the fundamental physical properties s, ρ and k can also be calculated.

Application Example

For an application example, a commercially available TEC is to be selected to cool a laser diode, which dissipates 5.5W and must be kept at 20�C for an ambient temperature of 25�C. It is also necessary to keep the heat sink as small as possible; in other words, the heat sink thermal resistance R_heatsink should be close to the maximum allowable heat sink thermal resistance R_hs-max.

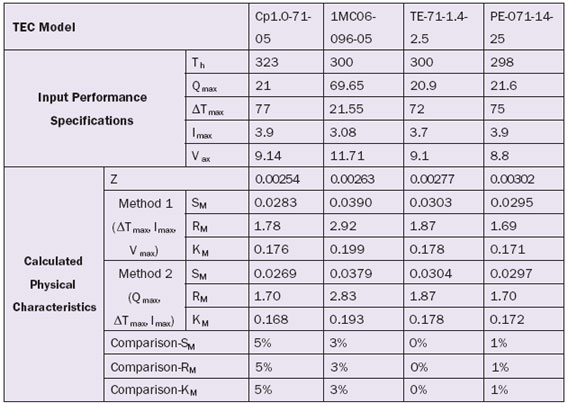
1) TEC Selection – As is known, Z is a criterion of a TEC’s ability to pump heat. Therefore, the Z value of different TECs from different manufacturers is calculated according to the information from the manufacturers’ catalogues. As shown in Table 2, the value of Z for the second TEC (1MC06-096-05) is in the middle. Considering other factors such as its smallest size, TEC 1MC06-096-05 is selected.

2) Determining Operating Parameters – The operating parameters for TEC 1MC06-096-05 are calculated for different DTs using the spreadsheet calculator (Table 1). The performance specifications (T_h, ΔT_max, I_max and V_max) shown in Table 2 for the selected TEC (1MC06-096-05) are entered along with the operating conditions (I, T_h, T_c, and T_a). The current, I, entered in the calculator is then adjusted until the calculated value of Q_c equals the specified heat load (i.e., 5.5W). The result of the calculations for each Δ T are recorded as shown in Table 3. As also shown in Table 3 for the example calculation, the value of allowable heat sink thermal resistance, R_heatsink, reaches its maximum value of about 2.57�C /W at a ΔT = 45�C. However, the bigger value of COP of 1.01 occurs at ΔT = 30�C, so this chosen as the design temperature difference.

Table 2. TECs from Different Manufacturers

Discussion about the Two Methods to Calculate S_M, K_M and R_M

Two methods to calculate S_M, R_M and K_M have been discussed in this article. Errors exist between the two calculation methods, and the biggest is 5%, as shown by Table 2. One reason is that our model, representing TEC operation, equations (8) and (9), is an ideal one and the TEC module parameters (S_M, R_M and K_M) are taken as constants. Actually, S_M, R_M and K_M depend on the temperature, more or less. Another reason is that the performance specifications from manufacturers are experimental results. Usually different manufacturers use different experimental methods under different conditions.

Table 3. Operating Parameters of TEC (1MC06-096-05)

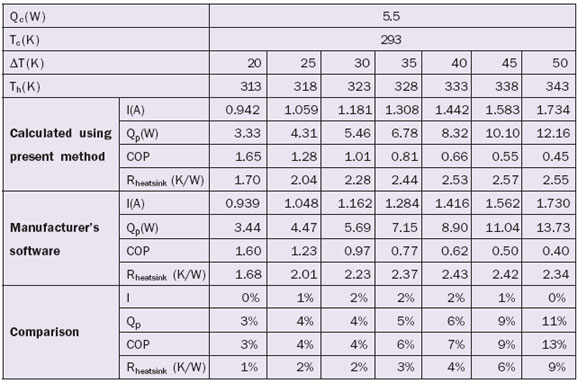Comparison with Manufacturer’s Software

In Table 3, calculated example results are compared with results from the manufacturer’s software. As may be seen some discrepancies do exist and the further T_h is from 300K (which is the hot side temperature at which performance specifications are given), the bigger the discrepancy for Q_p. This is because Z, S_M, R_M and K_M are not always constants as stated before. Actually, Z, S_M, R_M and K_M are dependent on the temperature to some degree. Notwithstanding this discrepancy, a difference below 10% is acceptable.

Surely, the manufacturer’s software would be expected to be more accurate. However, not every manufacturer provides software. Although performance curves can sometimes be used in place of calculations, most often performance curves are given at a specific T_h, for example, 25�C or 50�C, which is usually different from in the application under consideration. Another problem is that reading off curves and performing the required iterations is tedious and troublesome, especially when many different ΔTs must be considered. Accordingly, the calculation method presented in this article may be quite useful due to its simplicity and convenience, especially for the initial estimates during the cooling design process.

Summary

A simple method to calculate the physical characteristics of a TEC and evaluate the performance of the TEC has been presented in this article. The comparison and discussion shows that some imperfections exist for the calculation method. Notwithstanding this, the calculation method is useful due to its simplicity and convenience, especially as an aid in the selection of a TEC and to obtain initial estimates of its performance in the desired application.

Acknowledgement

The author wishes to thank the editor Robert Simons for his efforts in improving readability. The author also wishes to thank the reviewers for their constructive comments of an earlier version of this article.

References

1. Simons, R. and Chu, R., “Application of Thermoelectric Cooling to Electronic Equipment: A Review and Analysis,” 16th IEEE SEMI-THERM symposium, pp.1-9, 2000.
2. Riffat, S., Ma, X., “Thermoelectrics: A Review of Present and Potential Application,” Applied Thermal Engineering, Vol. 23, pp. 913-935, 2003.
3. Lee, H., Yoon, J., Kim, C-J, “Numerical Analysis on the Cooling of Laser Diode Package With a Thermoelectric Cooler,” Heat Transfer- Asian Research, Vol. 30, Issue No. 5, pp. 357-370, 2001.
4. http://www.peltier-info.com/manufacturers.html
5. http://www.melcor.com/
6. Huang, B., Chin, C. and Duang, C., “A Design Method of Thermoelectric Cooler,” International Journal of Refrigeration, Vol. 23, pp. 208-218, 2000.
7. Chein, R. and Huang, G., “Thermoelectric Cooler Application in Electronic Cooling,” Applied Thermal Engineering, Vol. 24, pp. 207-2217, 2004
8. Rowe, D., “CRC Handbook of Thermoelectrics,” CRC press, Inc., 1995.
9. Gierscheck, J. and Johnson, D., “Latest Developments in Thermoelectrically Enhanced Heat Sinks,” ElectronicsCooling, Vol. 11, No. 3, August 2005.
10. Simons, R., “Application of Thermoelectric Coolers for Module Cooling Enhancement,” ElectronicsCooling, Vol. 6, No. 2, May 2000.
11. Simons, R., “Effect of Improved Thermoelectric ZTs on Electronic Module Coolability,” ElectronicsCooling, Vol. 12, No. 4, November 2006.