Thermal analysis tools available to engineers and scientists offer a wide variety of methods to solve problems. A cursory review of the past decade’s issues of ElectronicsCooling magazine can show methods ranging from analytical techniques (such as hand calculations) to spreadsheets to full numerical/computational solutions such as CFD (Computational Fluid Dynamics) and FEA (Finite Element Analysis).
Although articles have discussed important basics such as how to use a particular method, and what to do to ensure sound results, the present authors note the issues of when or where to use any particular method have not been discussed as thoroughly. A few articles in the literature have partially addressed this (see [1]-[2]). Often thermal engineers do use a method appropriate to the problem, but as a group default to a method or technique that is comfortable and familiar. A better solution method may be available but not considered because of this bias. Due to this normal characteristic of human behavior, it is time for a careful examination of the methods available today, and for strategically using different methods (the when or where of the method, which means understanding the underlying why one method may be best).
CLASSIFICATION OF PROBLEM
The best place to begin deciding what type (or multiple types) of solution method may be preferred is to classify the problem to be solved. The two classification methods used for this article will be examining the geometry definition of the problem and the goals of the thermal model.
This means understanding two things clearly: what type of information is available at the problem definition; and the end goals of the solution. Examining these two areas will tend to point one in a specific direction. They also will point out the possibility of other solution methods and the advantages they may contain over one’s typical method.
Geometry definition is a statement about how much detail about the geometry is known at the time the problem is to be solved. Anyone who has been involved in a variety and significant number of projects has seen a wide range in this category. Often thermal analysts have been brought in late to solve an issue after the entire project is nearly complete; in these cases the geometry is well defined and often thoroughly detailed in explicit CAD models with complete bills of materials. One could label these as “fully defined” geometry definitions.
Sometimes thermal issues are addressed early in a design process, and in these cases very little may be explicitly defined. The analyst may know there will be some number of PCBs, and that the overall product dimensions will be about x by y by z, and that the enclosure will have certain features typical of the product class, but perhaps little is known beyond that. The thermal dissipation may even be only roughly known and may have a wide possible range owing to product features being not well defined. Such a situation could be described as a “nebulous” geometry definition, or architecture phase.
Certainly some combination of the “fully defined” and “nebulous” cases exist, and often this is found in many design situations. Perhaps the PCB is an existing item and will be reused in a new product, so it is well defined while the remaining design around it is mostly unknown. This condition will be labeled as the “partially defined” geometry definition.
All three of these conditions encompass the full range of geometry definitions one may find when beginning a thermal analysis, and as the authors explain, it is beneficial to consider the starting point when making a choice of tool for the analysis.
The second problem classification revolves around the goals of the thermal model. These may change over time. The thermal model goal typically falls into one of two broad categories.
The first goal category could be called the multiple-scenario or design trade-off study. In this situation, there may be several types of solutions that could be used to solve the thermal problem. Each type of solution may be quite different from other ones in geometry, material or type of cooling system. Changes to design strategies or thermal paths may be significant among the options. Adopting a particular solution in one design may involve a trade-off with other desirable features from another.
For example, one could examine a product that is a chassis with internal electronics. Perhaps the design could be cooled by natural convection; this requires a certain surface area and possible ventilation openings. Care would be required to place heat sinks, components, etc., in the appropriate places for cooling. Touch temperatures may also need to be considered. The same product could also be cooled by forced convection. In this case, fan placement, air inlet and outlet sizes, and noise requirements all must be evaluated. The installation of the product in its environment also factors into the product solution; blowing hot exhaust air onto an end user would not be suitable for most products. Other variables besides these can also be important, but this example shows that some thermal modeling goals may have numerous starting points. Ultimately this type of problem requires evaluating many geometries and finding the thermal performance of each one.
A second goal category could be called fully specified. In this case, there are few types of solutions to examine, but they are detailed designs. This is common in later project phases when a particular solution has been chosen. While chassis designs and layouts may be close to final form, some smaller details may be undecided, such as type and placements of thermal interfaces, heat sink fin spacing, effect of gap pads, or rearrangement of PCB hot components. Once a product final design is completed, a final thermal analysis is often performed as part of the product launch verification, and would also fit this category.
SOLUTION METHODS FOR PROBLEM CLASSES
With these classifications and goals in mind, one can then examine the solution methods available and see that there are some reasonable fits between the problem and type of solution method. This is an important step. One mistake people tend to make is to use and re-use methods they are most familiar with rather than what may be most suitable. This leads to forcing a method or tool to solve the problem. While this will still lead to solutions, it is not necessarily the best manner to go about this process. From this viewpoint, the authors propose the following matches of methods to the problem classes previously described:
Numerical Analysis with Systems of Fundamental Rquations for Nebulous Geometry or Multiple Scenarios
When geometry is largely unknown, or multiple scenarios must be evaluated, it is most efficient to keep factors set to a variable or numerical value to allow for faster changes. For example, the convective surface area of an enclosure could be represented by number (say .25 m2), or it could be explicitly modeled in 3D CAD. If one wished to change this area to 0.3 m2, this is an easy change if it is just a variable in an equation; the change becomes much harder if the 3D model must be changed (and this becomes cumbersome if several variables have a number of values to be evaluated).
To use this method, systems of fundamental, simultaneous equations are written and solved. In the authors’ experience this is tractable if the number of equations and unknowns is under 25 or so; beyond that may be difficult to set up and solve effectively, depending on the solution algorithm. The equations are forms of the three basic heat transfer equations for conduction, convection and radiation familiar to the reader:
kA
l(T1 – T2)
Q=hA(T1 – T2)
Q=σAfε(T14 – T24)
A key point here is that the heat flow path must be visualized enough to write the equations correctly. The visualization exercise is an extremely powerful thought and discussion tool. The solved equations serve to quantify the relative heat flow paths, identifying trouble spots and opportunities for improvement. Of course, the accuracy of the results depends heavily on the accuracy of the thermal network. Sometimes several versions of the network are needed to arrive at a suitable representation — just as several versions of experimental or computational models are needed to achieve confidence in the model. Also, sometimes the accuracy of the solution is less important than the ability to quantify relative effects in order to make a good design decision. For the design decision, the ability of the network to capture the effect of a design variation is key.
To solve the system of equations, software that is essentially high level programming (e.g., commercial codes such as MATLAB or Mathcad, or network solvers such as the SPICE codes for solutions) is well suited to the analytical method. Figure 1 shows a sample problem set up using Mathcad. Author Petroski has used this method for small electronic devices dissipating a few watts to much larger electronic cabinets of 1kW dissipation with good correlation to product tests.

The network equations can also be implemented in spreadsheet form if needed, see [4]. There are many powerful programming tools available in spreadsheets far beyond simply coding formulas using cell references with row and column indicators. The biggest advantage of spreadsheet analysis is that the software is available on nearly every computer as part of an office software suite, requiring no additional purchase or installation. This feature facilitates sharing and discussion with team members who are not thermal specialists. A disadvantage of solving the network equations in a spreadsheet is that the solution equations must be coded afresh if there are changes in number of nodes, or in the way they are linked together. Also, since everything is done manually, debugging and assessing the suitability of the network are entirely up to the user. Another disadvantage to spreadsheets is that non-linearity in the equations (for example, properties that depend on temperature) can be tricky to handle, although there are ways to include these effects that are beyond the scope of this article.
Numerical Analysis with Discretization for Nebulous Geometry or Multiple Scenarios
Solving the same type of problem as the previous case is possible with a resistance network that would discretize the model into more regions. It also may allow for easier solutions with other programming methods; some non-linear areas of a problem may be translated into linear forms without much loss of fidelity. For example, a flat plate with a small heat source may contain spreading resistances; such a problem may be handled by discretizing the region into smaller regions with the appropriate conduction equations (see [3] for such equations). Such a problem could allow for multiple spreading scenarios to be examined without using a single equation for spreading and possibly violating its assumptions. Viewed another way, perhaps a design may or may not incorporate spreading as a significant contribution to the heat transfer. A discretized region that can incorporate spreading, or not, by using the conduction equations may simplify solving the model for a variety of materials and geometries.
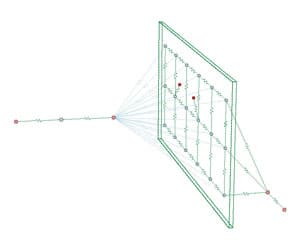
For this method, solutions can be found with many of the same network solution techniques described in the previous section. Another class of solvers known as finite difference solvers can be used and thermal versions of such programs (SINDA is a well-known example) provide the advantage of thermal resistance elements for each type of heat transfer, along with debugging and solution assessment.
Hybrid Solutions for Partially Known Geometry and Some Trade-Off Studies
When some of a problem’s geometry is well-defined, a combination of a fully discretized solution and some ability to handle unknown geometry is useful. For example, one may have a PCB or electronics module whose design is complete, but whose surrounding chassis or enclosure design is not defined. The two previous methods work well for the unknown area of the design where single or small numbers of nodes represent major sections of it. A well-defined numerical model can be used for the known module.
These two types of models then need to be combined for a solution. With the proper heat transfer equations one can connect these two parts. Perhaps the simplest manner to model this is to use the finite difference modeler. A discretized model is feasible for the well-defined portion of the model, and simple thermal resistance elements make up the connections to the undefined areas and the undefined geometry as well. As an example, see Figure 2. A portion of the model is well discretized and defined, while the rest of the model is composed of few elements. Model creation, with the solutions for different scenarios, is a straightforward process. The flexibility this approach provides for the unknown geometry is useful to find a final design that should meet the system temperature requirements, while providing good fidelity for the known geometry thermal profile.
Automated Numerical Solutions for Fully Defined Geometry and Fully Specified Goals
The final case is where the geometry of the problem is fully defined. This occurs near the end of the development when full CAD-based geometry is complete. At this point, a fully automated numerical solution is feasible with a complete discretized grid or mesh and appropriate boundary conditions, material properties, thermal loads, etc., applied. Any of the commercial or academic codes from the finite element method, computational fluid dynamics or the finite difference method can be used for this solution type. For this solution, the goal is often a final or near-final analysis of the problem and iterations for geometry changes or different scenarios are usually few or none. The greatest detailed solution is found with this method, but at the cost of knowing the final design and often is the longest solution time.
CONCLUSIONS
There are several methods to solve any thermal analysis, but given the different levels of geometry definition one can face, and the different types of goals for the end analysis, it is best to choose a solution appropriate for the class of the problem. Different solution methods have different advantages, and one should choose a method best compatible with the end goal(s). Ideally one should choose a solution method that provides the best efficiency for the type of problem at hand. This will assist in avoiding approaches that resemble the proverb, “If you only own a hammer, everything looks like a nail.” CFD is a fine problem solver, but if one is looking to evaluate multiple scenarios and many geometric conditions, a situation where dozens of analyses may result in weeks passing before everything is evaluated where another modeling approach would complete the task in hours or a few days.
Another drawback of using CFD directly is that fundamental limitations to the problem aren’t flagged, whereas the thought process required by model construction forces identification of the limiting factors. Thus, evaluating the basics first is also important — one could do a lot of modeling, only to find that the constraints are infeasible. This leaves the engineer doing a great deal of work with no result or poor results, and may be likened to using a hammer to pound in a screw, to alter the proverb. Simpler methods often identify important features and point to the solutions without resorting to extensive modeling.
References
[1] Luiten, G.A., “Cooling of a Flat TV Monitor”, ElectronicsCooling, Vol. 9 No. 2, May 2003.
[2] Luiten, G.A., “The Better Box Model”, ElectronicsCooling, Vol. 15 No. 3, August 2009.
[3] Lasance, C., “How to Estimate Heat Spreading Effects in Practice”, Journal of Electronics Packaging, 031004, Vol. 132, September 2010.
[4] Wilcoxon, R., “Calculation Corner: A Spreadsheet Based Matrix Solution for a Thermal Resistance Network, Part 1”, ElectronicsCooling, Vol. 16 No. 3, September 2010.
[5] Equation system developed and solved in Mathcad software by PTC.
[6] Model produced in Sauna MS software by Thermal Solutions.
[7] Belady, C., and Minichiello, A., “Effective Thermal Design for Electronic Systems”, ElectronicsCooling, Vol. 9 No. 2, May 2003.






