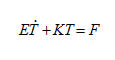Thermal management is an increasingly important consideration in the development of power electronic systems. Electro-thermal simulation is required at the system level in order to ensure under realistic loads the fulfillment of thermal requirements, which strongly influence the performance, reliability and efficiency. A significant modeling issue is to obtain a compact but accurate thermal model needed for the system level simulation. We suggest an efficient methodology based on modern mathematical algorithms of model order reduction (MOR), and demonstrate the approach on a power MOSFET model.
Electro-Thermal Simulation
Electro-thermal simulation at system level is a combined simulation of electrical and thermal aspects of the system as schematically shown in Figure 1.
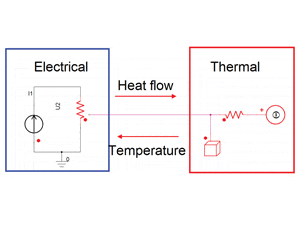
The circuit model calculates power dissipation, which is used by the thermal subsystem to evaluate the temperatures. Temperatures in return influence the circuit parameters, thus requiring a two-way coupling.
The thermal model in Figure 1 is a simple, lumped-element model. For general complex geometries, a more accurate, physical model in form of heat transfer partial differential equation is required:
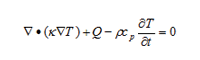
where K(r) is the thermal conductivity in W/m/K at the position r, cp (r) is the specific heat capacity in J/kg/K, ρ(r) is the mass density in kg/m3, T(r,t) is the temperature distribution and Q(r,t) is the heat generation rate per unit volume in W/m3. Spatial discretisation (via e. g. finite element method – FEM) of (1) results in a large-scale ordinary differential equation (ODE) system with n equations of the form:
where E Є Rnxn is a heat capacity matrix, K Є Rnxn is a heat conductivity matrix, T Є Rn is a vector of nodal temperatures in time and F Є Rn is a heat source load vector. (1) can also be considered as an electrical network where the vector T will be equivalent to unknown voltages, the matrix E will be a capacity matrix and the matrix K the resistance matrix (see [1] for methods to synthesize electrical networks). In both cases, (2) is not compatible with system level simulation, as vector T usually contains several hundred thousand degrees of freedom. The remedy is to apply modern mathematical algorithms of model order reduction [2],[3], which enable a formal transformation of (2) to a low-dimensional ODE system of the same form but with much smaller dimensions, as described in the following section.

Model Order Reduction
Model order reduction is an area of mathematics that enables a formal approximation of the physical model and hence, the generation of a compact model suitable for system level simulation (see Figure 2).
Model order reduction starts with the ordinary differential equation system (2), which is slightly modified as follows:
In (3) the load vector F Є Rn from (2) was split into a product of a constant input matrix B Є Rnxp and a vector u(t) Є Rp of p input functions (heat sources) and a second, output equation has been added. The output equation in (3) defines certain linear combinations of the state vector T that are of interest for the particular application in system level simulation. This equation has to be defined by the user. Note, that in a case when the complete temperature field is required, the output matrix C Є Rmxn (where m is the number of outputs of interest) has to be defined as a unity matrix.
Model reduction is based on an assumption that the “movement in time” of a high dimensional state vector T can be well approximated by a lower dimensional subspace (ε in Figure 3 should be small). Such subspace is defined by the projection matrix V. Provided this subspace is known, the original system can be projected on it, as shown in Figure 3.

The definition of such low dimensional subspace, i. e. matrix V, is subject of a particular MOR algorithm. For thermal systems, we propose to use the Krylov-subspace based Arnoldi algorithm [7], which defines the projection matrix in such a way, that the transfer function of the original dynamic system is well approximated by the Taylor-series of the transfer function of the reduced system. Mathematically speaking this approach belongs to the Padé approximation and is also known under the name moment-matching method, where the Taylor-series coefficients are called moments. The detailed description of the algorithm and the theorems proving its moment matching properties can be found in [2][3] and [7].
For performing model order reduction of finite element models, we employ the software tool MOR for ANSYS [4]. It reads the system matrices created by the finite element simulator ANSYS [5], runs the Arnoldi algorithm and writes the reduced system, i. e. its matrices, Er, Kr, Br and Cr (see Figure 3). The reduced matrices can be read directly in Simplorer [6], MATLAB/Simulink, and other system level simulation tools. It is also possible to write down the reduced model as a Spice model or a template for the use in VerilogA and VHDL-AMS.
Electro-Thermal System Simulation of a Power MOSFET

The self-heating of a power MOSFET can cause a significant temperature rise associated with temperature gradients and thermal stresses in the particular device. Thermal cross-talk between transistor channels as well as temperature dependent heat generation rates will accelerate the self heating phenomenon, which can occasionally even cause a thermal runaway instance. A good understanding of the electro-thermal behavior of the power switch, electronic control unit and the load is a key for the system design.
The model generation path and electro-thermal system simulation are demonstrated for a novel High-Side Switch device [8] with four independent channels. The device is packaged in a Small Outline IC (SOIC) package, which itself is assembled onto a printed circuit board. Figure 4 shows a model of the de-capsulated package (plastic molding compound removed) with the wire bonds connecting each transistor channel with its associated external lead fingers.
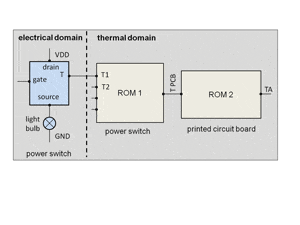
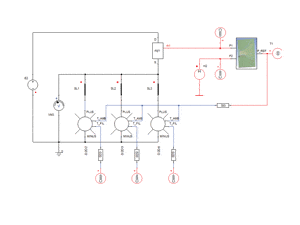
The corresponding electro-thermal system model (Figure 5) contains two distinct thermal submodels for power switch and printed circuit board (PCB), and five electrical submodels, one for each transistor channel and one for the light bulb. Thermal submodels have been extracted from the 3D-finite element models by means of model order reduction, as described in section 2. Power switch and PCB share one common node at the system level, which represents the thermal port between SOIC exposed pad and the adjacent PCB land pad. The PCB model also contains the heat convection of the system into the ambient air.
The electrical transistor models are ready to consider dynamic self heating phenomena. In addition to the electrical IO/s, gate, drain and source, these models each contain one electro-thermal port T interconnecting electrical and thermal domains of the power switch.
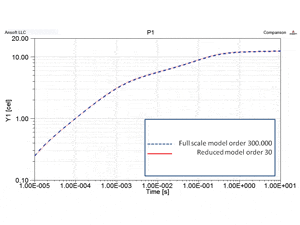
In Figure 6, the thermal response of a full-scale model and of a reduced order model of a single transistor is shown. The difference is less than one percent. Model reduction takes only 80 s, while transient simulation with 60 time steps requires about 2000 s. At the same time, system level simulation lasts less than a second.
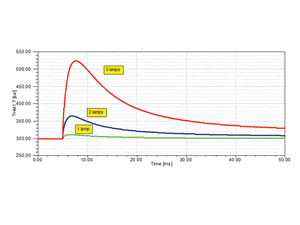
In the system level model shown in Figure 7 a single transistor has been loaded sequentially with one, two or three lamps. The light-bulb model is represented using an existing Spice model which was imported directly. In Figure 8 the junction temperatures are shown as functions of time for a different number of lumps. One can see that with three lumps the temperature for short time of about 5 ms goes over 200 degrees Celsius. The thermal model considered in this study cannot tell us whether this is acceptable or not, but it demonstrates the need for transient electrothermal simulation. The stationary temperatures are acceptable for all three curves in Figure 8 and only transient simulation can reveal that the temperature goes over the critical temperature.
More information can be found in [9] and [10].
Conclusion
We have shown that model order reduction is an efficient tool to automatically generate an accurate compact thermal model for power electronic devices. The advantages of the method are as follows:
-
Figure 7. Simulation model with bulb lamps. The method uses the system matrices from the accurate finite element model directly.
- The method is automatic. The user should set the dimension of the reduced model and define the outputs of interest. According to our experience the accuracy of one percent is achieved with 10-15 degrees of freedom per input.
- The model reduction process is fast. The time for model reduction is comparable with that of a static solution and usually, depending on the chosen integration time step, shorter than a single transient run with the original finite element model.
REFERENCES
[1] J. T. Hsu, L. Vu-Quoc, A rational formulation of thermal circuit models for electrothermal simulation. Part I: Finite element method. IEEE Trans. Circ. Syst. – I: Fund. Theor. Appl. v. 43, N 9, p. 721-32, 1996.
[2] T. Bechtold, E. B. Rudnyi, J. G. Korvink. Fast Simulation of Electro-Thermal MEMS: Efficient Dynamic Compact Models, Springer 2006, ISBN: 978-3-540-34612-8.
[3] A. C. Antoulas, Approximation of Large-Scale Dynamical Systems. Society for Industrial and Applied Mathematic, 2005, ISBN: 0898715296.
[4] E. B. Rudnyi and J. G. Korvink. Model Order Reduction for Large Scale Engineering Models Developed in ANSYS. Lecture Notes in Computer Science, v. 3732, pp. 349-356, 2006, http://ModelReduction.com.
[5] ANSYS® Mechanical, Release 13.0, http://www.ansys.com
[6] ANSYS Simplorer®, Release 9.0, http://www.ansys.com
[7] R. W. Freund, “Krylov-subspace methods for reduced order modeling in circuit simulation,” Journal of Computational and Applied Mathematics, vol. 123, pp. 395-421, 2000.
[8] MC15XS3400: Quad High Side Switch, http://www.freescale.com
[9] T. Hauck, W. Teulings, E. B. Rudnyi. Electro-Thermal Simulation of Multi-channel Power Devices on PCB with SPICE. THERMINIC 2009, 7-9 October, Leuven, Belgium, 6 p.
[10]
T. Hauck, I. Schmadlak, L. Voss, E. B. Rudnyi. Electro-Thermal Simulation of Multi-channel Power Devices: From Workbench to Simplorer by means of Model Reduction. NAFEMS, Seminar: Multi-Disciplinary Simulations – The Future of Virtual Product Development, 9-10 November 2009, Wiesbaden, Germany, paper #5, 10 p. l