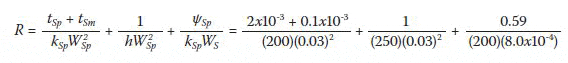The purpose of the present article is to suggest that accurate solution of thermal spreading problems for multilayer, edge-truncated geometry is easily accomplished using free, open-source finite element software. This should be especially attractive to designers and analysts who are full-time independent consultants, temporary contractors, or regularly employed engineers desiring to free themselves from the problems of justifying the cost of infrequently used software. This writer has studied some of the available open-source software and believes that many readers will profit by the information in the following paragraphs.
Background
Thermal spreading resistance is usually defined as the temperature difference per unit heat transfer, e.g. K/W, between a source and a defined isothermal plane, point, or ambient temperature. Math models for steady-state thermal spreading resistance have been under development for several decades. Early models considered conduction to an isothermal reference plane and were therefore of limited use for analyzing electronic packages [1]. Lee described a transistor-on-heat sink application with a convecting and/or radiating surface [2,3]. In this case, a uniform total heat transfer coefficient h was assumed for an ambient temperature TA. The simplest of these models presumes a circular source centered on the surface of a circular substrate, a model that is accurate for many applications. Ellison published design curves and formulae for the maximum resistance (source center to ambient) for rectangular sources centered on rectangular substrates, either or both with non-unity aspect ratios [4]. Design curves were later added for source-averaged thermal resistances [5]. Time-dependence was added to the rectangular device problem by Rhee and Bhatt [6] who implemented a three-dimensional Green’s function solution based on a catalog of solutions by Cole et al. [7].
Both the steady-state and time-dependent models for three-dimensional conduction problems result in infinite series solutions: a single series for the Lee and Rhee solutions and a double series for the Ellison solutions. While the series formulae are not particularly difficult to implement in a math-scratchpad computer program, there is always the desire to use approximate closed-form formulae, i.e. non-infinite series based. Lee was successful in creating these approximations for his circular-shaped devices [2]. Continuing in the effort to obtain useful modeling results with approximate formulae, Lasance has proposed a method for calculating the spreading resistance for two-layer problems where the layers have unequal dimensions except for the thicknesses [8,9,10]. In these situations where the planar dimensions of the layers are not equal, there are no established closed-form analytical methods. Consequently, the engineer must often rely on more advanced numerical modeling using finite difference (FDM) or finite element (FEM) methods. Yovanovich and co-workers have also published numerous studies on spreading and closely related topics [11].
Sample Spreading Problem Geometry
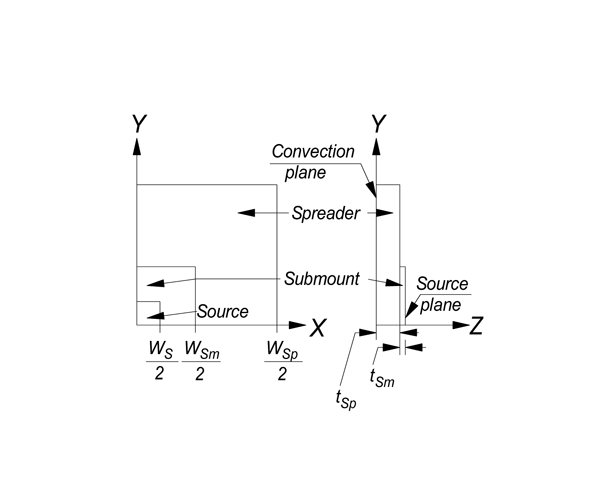
Lasance considered the test case of a two-layer spreading problem with a truncated-silicon top layer submount (planar dimensions less than bottom layer), on a copper-tungsten heat spreader as shown in Figure 1 [9]. The source plane is at the top of the submount and all surfaces are adiabatic except the source region and the Z=0 plane, the latter location modeled by a uniform heat transfer coefficient h. Lasance refers to this h as effective as it may include the effect of an area-enlarging factor due to a heat sink, a common practice in modeling electronic equipment [5]. In the present problem, h = 250 W/(m2·K), the same value Lasance used for some of his work. An ambient TA = 0 and a one watt total source dissipation mean that the maximum computed temperature is numerically identical to the thermal resistance. The square source is centered on a square, two-layer substrate, but symmetry allows the analysis of only one quadrant, thus indicating a corner source. Further advantage of symmetry could be used with the FEA model by halving this quadrant with a diagonal between the source and opposite corners. Table 1 lists the variable parameters used. A source of 1.0 W is uniformly distributed over the entire source area (8.0×10-4 m)2 as a heat flux of 1.5625×106 W/m2.
Case 1 is a benchmark comparison of analytical and FEA solutions and is used to justify the FEA model mesh for Cases 2-5. The top layer is not truncated for Case 1 and has the same conductivity as the bottom layer, i.e. this is a single layer material. Cases 2-5 are those in which we are primarily interested.
Simple Spreading Calculation for Case 1
The benchmark calculation for Case 1 uses rectangular device spreading theory from Ellison to obtain the dimensionless source center and source-averaged spreading resistances ψSp = 0.59 and ψAve-Sp = 0.50, respectively [5]. Theory shows that the maximum total thermal resistance from the source center to ambient is the sum of terms for one-dimensional conduction, uniform h convection, and spreading [5]:
Similarly, using ψAve-Sp, the total source-averaged resistance is
RAve = 7.58 K/W
The source center resistance, R, will be compared with an FEA calculation in the Results section.
Software Used and the Spreading Model Described
Two free of cost, open-source programs were used: (1) Salome [12] and (2) Elmer [13]. In the Windows version, Salome is used primarily for model building and meshing [12]. The Salome software has a rather complete set of plate and solid model features, but is not a complete CAD system. Some users might find themselves frustrated by the geometry module, but it is quite adequate for many applications. Perhaps the most inconvenient aspect is that once added, an object’s dimensions cannot be changed. Thus if you have an incorrectly sized object, you must delete it and try again. This is not much of a problem and if you prefer, an open-source CAD program is also available [14].
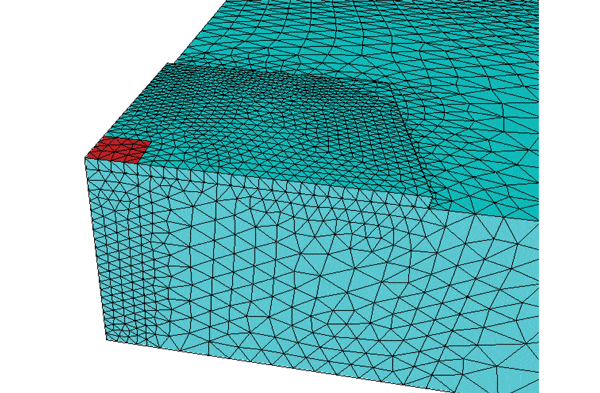
In the current spreading problem, Salome was used to build, mesh, and export the models. A look at Figure 2 for Case 3 shows that each model is constructed from three-dimensional blocks: a submount block, a spreader block, and a source block, the latter superimposed at a corner. The submount planar dimensions all differ for Cases 2-5. However, Cases 3-5 have truncated submount dimensions, i.e. the submount does not fully extend out to the spreader edges – a problem that is not managed by any of the analytical solutions of Ellison and Lee.
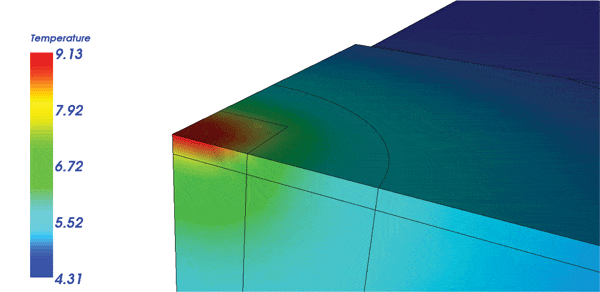
The source block has a total thickness that is the sum of the submount and spreader thicknesses. The top surface of the source block is the region to which the heat flux is applied (colored red in Figure 2). If the source, submount, and spreader blocks were left as-is in Salome, the geometry would consist of a single material. The “Geometry-Partition” operation must be used to separate the system into the three distinct objects. A later operation, “Geometry-Group” or “Mesh-Group,” is used to combine the lower portion of the source block with the spreader, and also to combine the upper portion of the source block with the submount, resulting in two distinct material groups. Two extruded circles are used to permit the creation of submesh regions with finer detail than that for the overall system. One of these cylinders is visible in Figure 3. Note that the mesh in Figure 2 shows the finest mesh in the source region, a not quite so fine mesh throughout the submount dimensions, and an even coarser mesh for the remainder of the spreader.
An “Explode” option is used to identify the various solid blocks and faces that can be grouped into the two different materials as well as the source and convection faces. The geometry and meshing efforts are completed by exporting the mesh to some suitable file structure, a good choice being the universal UNV type. The next step is to convert this file to a mesh file that is recognizable by the solving program, Elmer [13]. The file converter is a command-type program known as “Elmergrid.” This program not only creates the correct input file for Elmer, but can also be used to clean up the UNV file.
The mesh file is loaded into Elmer, which has a very complete set of options for input, in this case heat conductivities, heat flux, and the heat transfer coefficient. The project is saved to the hard drive and a simple click of a solver icon begins the solution process. Once a successful solution is obtained, one can use either of two different Elmer options to display results. For example, the “run-vtk” post-processor was used to produce Figure 3.
Spreading Results
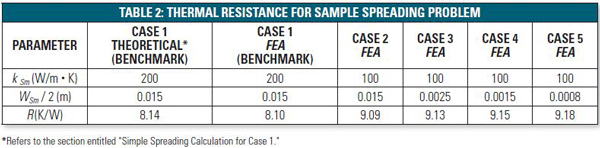
The theoretical and FEA results are listed in Table 2. The Case 1 benchmark, Theoretical and FEA results, have a discrepancy of 0.5%. The Case 1 theoretical and FEA discrepancy for the third term, RSp = ψSp/kWS, of the total resistance is 1.2%. These discrepancies are sufficiently small to justify the mesh. Note that for Cases 2-5 the resistance increases only slightly as the heat spreader planar dimensions decrease. A portion of the thermal surface contours in the vicinity of the source is shown in Figure 3, for which the legend is left with non-integral values so that the maximum temperature, i.e. the resistance, is displayed. In this case the submount is about six times the size of the source dimension and it is very clear that the size of the submount can be substantially decreased without significantly increasing the thermal resistance. The smallest submount configuration evaluated has dimensions of only twice those of the source and yet the thermal resistance is hardly different than that for Case 2, which has a non-truncated submount. These observations are entirely consistent with the surface temperature colors in Figure 3. The analysis also demonstrates the advantage that graphical results have over the single-value “theoretical” calculation used for the benchmark.
With regard to studies by Lasance in an evaluation of the application of single layer spreading formulae to multilayer problems, we can see in Figure 3 that use of the submount dimensions considered herein as a source for the second layer would be a poor modeling choice because such source dimensions would be too large.
No attempt has been made to address model approximations, but one of the omissions in this study is the absence of convection cooling from the submount and spreader planes on the source side of the device. This feature would be easy to add to the FEA model.
More Complex Conduction Problem – Single Chip Package on PCB Coupon
The thermal spreading problem considered in the preceding paragraphs has very simple geometry. As an example of a more complex problem, a single chip package attached to a circuit board coupon is shown with results in Figure 4. The geometry was constructed using the “Free-cad” open-source software [14]. While the author of this software stipulates that the program is under continuous development, it was more than sufficient for this problem and makes up for the limited model construction capabilities of Salome. In particular, it is helpful that Free-cad object dimensions are easily modified. The Free-cad STEP file export feature was used to create a file for import into Salome. From that point on, geometry meshing and model solving is similar to procedures used in the spreading example. Note that the substrate geometry was submeshed to obtain a finer mesh. The heat dissipating chip is not visible because it is mounted on the underside of the substrate.
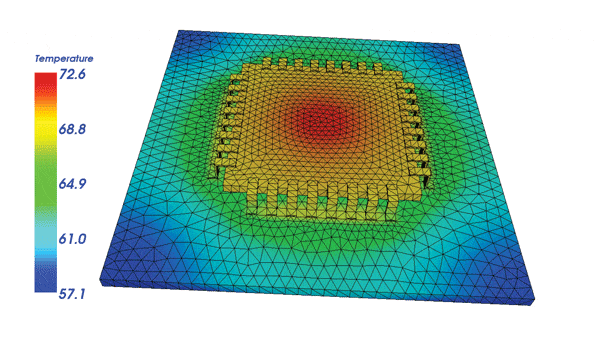
The legend for the IC package results in Figure 4 is left with non-integral values so that the maximum temperature (at chip source center) is displayed. This same problem was constructed and analyzed with commercial CAD and FEA software, for which the model and results are shown in Chapter 1 of [5]. The two different FEA programs were used to obtain a maximum temperature rise above ambient with about one percent discrepancy, a value that is probably due to mesh differences.
Summary and Comments
The FEA method permits the analysis of geometry that is too complex for analytical spreading formulae, most of which are infinite series solutions that cannot accurately account for multilayer structures with one or more edge-truncated layers. The chip package on PCB in Figure 4 is a moderately complex example solvable using most FEA codes. The reader inexperienced in FEA is cautioned to check for grid independence of the numerical solution, particularly when there are large scale differences in the geometry.
Details of using the open-source software have been largely omitted in this article because of space limitations. However, it is hoped that the reader will be pleased to learn of the programs introduced. The web can be searched for tutorials, though some of these may not be in the field of interest. Nevertheless, there may be sections of any tutorial that are of general use for modeling and meshing. In particular, there are many Elmer tutorials provided as part of the download package. The number of Salome tutorials is more limited. Finally, don’t let the name “Free-cad” lead you to think that it is not a serious program. Though it may not yet meet the needs of someone requiring a commercial grade tool, it is still very useful. The Appendices will be of interest if you choose to evaluate the software for yourself.
Appendix i: Salome Options and Suggestions
1. In the Salome menu bar, you will need to select Geometry or Mesh from the drop down Salome list, depending on what you want to do.
2. When you create your first geometric entity or load a CAD file, you need to right click on Geometry and select “Show” in the Object Browser to visualize the problem. You will also have to click on a “magnifying glass” icon to fill the display window. A similar procedure applies to viewing a mesh.
3. Geometry – Operations – Partition: you need this operation to separate the various geometric blocks into distinct parts, which otherwise will be a single material.
4. Geometry – New Entity – Explode: use this to “explode” the various geometric entities into solid parts and faces, the latter being necessary to apply boundary conditions.
5. Mesh – Create Mesh – Algorithm (use Netgen 1D-2D-3D): in the Object Browser, select your partition (Partition_1 by default) on which to create the mesh.
6. Compute: in the Object Browser, right click Mesh_1 (the first default name) and select “Compute.”
7. While in the Mesh option, create mesh groups to isolate individual materials and boundary faces.
8. Note that in Figure 4 the substrate has a different mesh density than the PCB. This was constructed by first creating the overall mesh, selecting Mesh_1, then selecting Mesh-Create Submesh option (with a greater mesh density), and right clicking Mesh_1 and selecting Compute. The submesh parameters can be edited and the problem remeshed without beginning again.
9. Export to UNV file: do this by right clicking Mesh_1 in the Object Browser and making the selection.
Appendix ii: Elmer Options and Suggestions
1. After you install Elmer, you may need to drag an ElmerGUI.exe to create a desktop shortcut icon.
2. Add a path to the Elmer executable, Elmergrid: Using Windows Explorer, select Computer, Properties, Advanced System Settings, Advanced, Environment Variables, Path, Edit, and then add the path to the Elmer installation directory. This will let you run “elmergrid” from any Command Prompt in any directory.
3. Create a desktop Command Prompt for convenience.
4. Use the Command Prompt to change to your model file drive and directory, then run Elmergrid without any arguments to get a list of options. A suggestion is to use “elmergrid 8 2 mesh_1.unv -autoclean,” where mesh_1.unv is the model mesh file.
5. In your first use of a mesh file, use Elmer – File – Load Mesh: select the folder “mesh_1” that was automatically created when you used Elmergrid. Don’t be confused by looking for a file. Elmer requires that you select a folder, not a file.
6. When you input model details for a heat problem, don’t forget to select Model – Equation – Add Heat Equation, and check the Active option.
7. After you have successfully solved a problem, if you use the Elmer “Post” icon, you may need to edit the background color to see all of the legend numbers.
Appendix iii: Other Suggestions
1. Free-cad, Salome, and Elmer are available as Windows binaries. Issues with regard to Windows 8 are presently unknown to the author.
2. The Ubuntu Linux distribution is easily downloaded as an ISO file, which in turn can be used to create a Linux boot-able system on a USB flash drive or DVD [15]. This distribution contains a large number of applications in addition to Free-cad, Salome, and Elmer. There is a Salome-Meca program that includes heat and elasticity modules, but the lack of complete manuals and the use of the French language in some parts of the software present obstacles for non-French readers.
3. The Linux CAE distribution is an alternate to MS Windows.
References*
[1] D.P. Kennedy, “Spreading resistance in cylindrical semiconductor devices,” J. Applied Physics, vol. 31, pp. 1490-1497.
[2] S. Lee, “Optimum design and selection of heat sinks,” in Proc. 11th Semiconductor Thermal Management and Measurement Symposium, San Jose, CA, pp. 48-54.
[3] S. Lee, “Calculating spreading resistance in heat sinks,” ElectronicsCooling, vol. 4, no. 1, Jan. 1998, pp. 30-33.
[4] G. Ellison, “Maximum thermal spreading resistance for rectangular sources and plates with non-unity aspect ratios,” IEEE Trans. Comp. and Pkg.Tech., vol. 26, June 2003, pp. 439-454.
[5] Gordon N. Ellison, Thermal Computations for Electronics, CRC Press, Nov. 2011.
[6] J. Rhee and A.D. Bhatt, “Spatial and temporal resolution of conjugate conduction-convection thermal resistance,” IEEE Trans. Comp. and Pkg. Tech., vol. 30, Dec. 2007, pp. 673-682.
[7] K. Cole, J. Beck, A. Haji-Sheikh, and B. Litkouhi, Heat Conduction Using Green’s Functions, Taylor & Francis, 2nd Edition, July 2010.
[8] C. Lasance, “Heat spreading: not a trivial problem,” ElectroncsCooling, vol. 14, no. 2, May 2008, pp. 24-30.
[9] C. Lasance, “How to estimate heat spreading effects in practice,” ASME Journal of Electronic Packaging, vol. 132, Sept. 2010.
[10] C. Lasance, “Two-layer heat spreading approximations revisited,” in Proc. 28th Semiconductor Thermal Management and Measurement Symposium, San Jose, CA, pp. 269-274.
[11] www.mhtl.uwaterloo.ca/MHTLarchive.html.
[12] www.salome-platform.org.
[13] www.csc.fi/english/pages/elmer.
[14] www.sourceforge.net/apps/mediawiki/free-cad.
[15] www.caelinux.com.
*This list of references is not all-inclusive as there are other publications to be found on the subject.
Bibliography
Gordon Ellison is a retired Tektronix, Inc. Fellow. Following his retirement from Tektronix, he has taught Electronics Cooling at Portland State University and consulted with local companies. His publications include the books Thermal Computations for Electronic Equipment, Van Nostrand Reinhold Publishing Co., 1984, reprint edition by Krieger Publishing Co., 1989, and more recently, Thermal Computations for Electronics, CRC Press, 2011. He is a past winner of the IEEE Semi-Therm Significant Contributor Award. He received a B.A. degree in physics from the University of California at Los Angeles, and an M.A. in physics from the University of Southern California.
