Man Prakash Gupta and Satish Kumar
G.W. Woodruff School of Mechanical Engineering, Georgia Institute of Technology
INTRODUCTION
Due to the growing demands of higher performance and faster computing, the number of cores in a microprocessor chip has been increasing consistently. The transition from single core to multi-core technology has already been observed in the past few years and with the strong potential of parallel computing, the transition from multi-core to many-core is also imminent where the number of cores on a single chip is expected to reach in hundreds or even thousands per single processor die. Such large-scale integration and very high power densities on chip will bring a significant challenge of heat dissipation. The traditional air-cooling methods begin to reach their flow and acoustic limits for very high power density (~1.5 W/mm2) apart from being inefficient from economic point of view when applied to many-core technology [1, 2]. Moreover, the uneven workload on the cores leads to spatiotemporal non-uniformity in the thermal field on chip which can be detrimental to its performance and reliability [3]. The leakage power also increases exponentially with temperature resulting in higher power dissipation, and cooling costs [4, 5].
Another way to obtain a uniform on-chip temperature distribution and lower peak temperature is efficient redistribution of heat within the chip which can help to improve the energy efficiency and coefficient of performance (~ compute/cooling power). This brings new opportunities for the dynamic thermal management (DTM) techniques, and their role to address the challenges of power dissipation in many-core processors becomes very important. Many DTM techniques have been explored such as clock gating, dynamic voltage and frequency scaling, and thread migration for single and multi-core processors [6-9]. All these reactive methods can have power and performance overhead apart from the hardware and software implications.
Power multiplexing which is a proactive method can be utilized as a supplementary approach to the reactive methods for effective thermal management of many-core processors [10, 11]. Power multiplexing technique involves redistribution (or migration) of the workload of the cores in the chip at regular time intervals to control the thermal profile on the chip. This approach is different from the reactive DTM techniques which wait for the temperature to increase beyond a certain threshold value. The idea is to improve the thermal profile by using idle or underutilized cores efficiently. The guiding rule which governs the redistribution of workload is called migration policy. The time interval at which this migration takes place is referred to as timeslice. A smaller timeslice corresponds to faster multiplexing. The value for the timeslice is typically chosen such that it is smaller than the characteristics thermal time constant (τ) of the system. In the present case, this time constant τ is defined as the time for the chip peak temperature to reach 63% of the steady-state after turning on the power under flow conditions described below. The value of τ is estimated to be 0.1s. This criterion for the timeslice selection is based on the requirement that the 2D effects of power multiplexing need to be realized faster than the 3D thermal diffusion in order to get full advantage of multiplexing. A tile-type homogeneous 256-core processor is considered where the cores are arranged in a 16×16 2D array [12]. The power dissipation value has been selected based on the prediction by International Technology Roadmap of Semiconductor (ITRS) for 16 nm node technology. The model considers 2 W of power dissipation in each active core which is reasonable for cores with 16 nm node technology running at 3 GHz. The total power dissipation on the chip is considered to be 128 W, i.e., at one instant only 25% cores (~64 cores) are active.
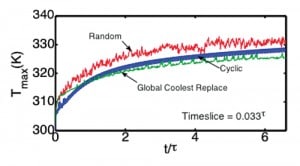
Three migration policies namely, random, cyclic and global policies are explored here (Figure 1). Random policy involves random redistribution of all active cores at each timeslice. In cyclic policy active cores are assigned in a checkerboard configuration and shifted in a circular fashion at each timeslice maintaining checkerboard configuration. Global policy involves the swapping of workload between hottest and coolest cores at regular time intervals.

METHODOLOGY AND RESULTS
Using computational fluid dynamic (CFD) detailed heat transfer analysis of the electronic package is performed. The computational domain is comprised of a flow duct, a heat sink, a heat spreader, the thermal interface material (TIM), a chip and a substrate (Figure 2) [12]. The properties of the various components of the system are considered to be constant and are listed in Table 1. It should be noted that temperature dependent thermal conductivity of the components does not cause any significant change in the results since the temperature variation is between 300 and 330 K only. The dimensions of chip are 12 mm x 0.5 mm x 12 mm and the typical size of a grid cell inside chip is 0.375 mm x 0.1mm x 0.375mm. A uniform velocity profile at the inlet of the air flow tunnel is considered with constant velocity of 5 m/s. An outflow boundary condition is imposed at the outlet of the tunnel and no-slip boundary condition is imposed at the walls of the tunnel and outer surfaces of the electronic package (Figure 1(a)). The flow inside the tunnel is turbulent as Reynolds number based on the inlet flow rate and duct hydraulic diameter is 20,000. As accurate turbulent flow computations are not critical in the present study, Spalart-Allmaras turbulence model [13] was used, which is a simple one-equation model and appropriate for applications involving wall-bounded flows and for avoiding fine meshing near the wall. We consider SIMPLE scheme for pressure-velocity coupling, implicit scheme for transient formulation and second order upwind scheme for the discretization of all governing equations [14].
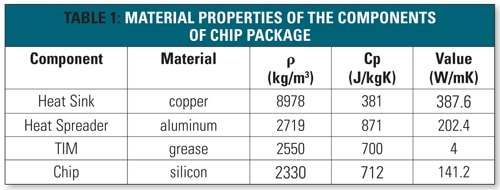
Three cases (slow, fast or no multiplexing) are investigated corresponding to each migration policy to examine the effect of timeslice variation. For random power multiplexing, results suggest faster multiplexing (at timeslice = 0.0033 τ which equals to 106 clock cycles) provides 10 °C reduction in the peak temperature (Tmax) and 15 °C reduction in the maximum spatial temperature difference (Tmax-Tmin) [12]. A graphic comparison of the thermal profile on the chip at time instant, t = 6.6 τ, is shown in Figure 3.
For cyclic policy, results indicate that it reduces the peak temperature by only 3 oC even for vary fast multiplexing. This small reduction can be attributed to the pre-existing checkerboard configuration of active cores. The maximum spatial temperature difference across the chip is however significantly reduced (by 7 oC).
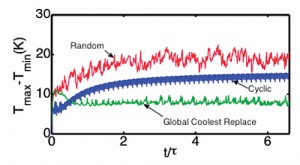
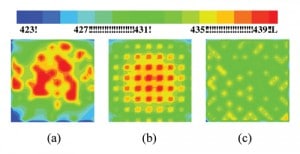
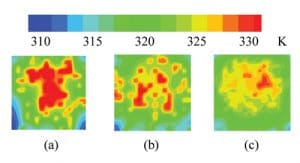
Global policy is intrinsically different from the previous two policies as it takes decisions based on the instantaneous chip temperature and also, fewer cores are involved in the multiplexing. To begin with, only a pair of cores is considered for the global multiplexing, i.e., the workload is swapped between the hottest and the coolest core at each timeslice. It is found that global policy shows significant improvement in thermal profile even for very slow multiplexing. Analysis of the power map at each migration step, finds that the global coolest policy ingeniously places the active cores away from the center of the chip such that it not only reduces peak temperature by a significant amount but also reduces thermal non-uniformity. By comparison of the three policies, it is found that cyclic policy shows better performance compared to random policy but global policy outperforms the other two in terms of higher peak temperature reduction and better thermal uniformity on the chip (Figure 4). A graphic comparison of the thermal profile on chip can be seen in Figure 5. It should be noted that increasing the number of cores involved in the swapping of workload during the global policy does not bring any significant improvement in the thermal profile of the chip [12]. Thus, the results advocate the strength of global policy as it requires swapping of workload on only a pair of cores and even slow multiplexing can get higher reduction in the peak temperature and uniformity in the temperature profile.
SUMMARY
Power multiplexing approach has been presented as a prospective thermal management technique for many-core processors. The global power multiplexing has been found to be the most effective among the three policies discussed in this article. The peak temperature reduction of 10 oC and the maximum spatial temperature difference reduction of 20 oC have been observed on a 256-core chip using global policy based power multiplexing. This can be attributed to its inherent approach to optimize the proximity of active cores on a finite size chip by automatically considering the effect of geometrical and thermal properties of the 3D system through the temperature distribution at each migration step. The work presented in this article may be considered as a first order analysis of migration policies as simple policies are applied in case of the homogeneous many-core processors. More evolved policies can be formulated to handle thermal management of heterogeneous many-core processors.
REFERENCES
[1] J. Michael J. Ellsworth, “High Powered Chip Cooling – Air and Beyond,” Electronics Cooling, 2005.
[2] P. Zhou, J. Hom, G. Upadhya, K. Goodson, and M. Munch, “Electro-kinetic microchannel cooling system for desktop computers,” Twentieth Annual Ieee Semiconductor Thermal Measurement and Management Symposium, Proceedings 2004, pp. 26-29, 2004.
[3] R. Mukherjee and S. O. Memik, “Physical Aware Frequency Selection for Dynamic Thermal Management in Multi-Core Systems,” in IEEE/ACM International Conference on Computer-Aided Design (ICCAD). , 2006, pp. 547-552.
[4] M. Janicki, J. H. Collet, A. Louri, and A. Napieralski, “Hot spots and core-to-core thermal coupling in future multi-core architectures,” in 26th Annual IEEE Semiconductor Thermal Measurement and Management Symposium (SEMI-THERM). , 2010, pp. 205-210.
[5] E. Kursun and C. Chen-Yong, “Temperature Variation Characterization and Thermal Management of Multicore Architectures,” IEEE Micro., vol. 29, pp. 116-126, 2009.
[6] D. Brooks and M. Martonosi, “Dynamic thermal management for high-performance microprocessors,” in The Seventh International Symposium on High-Performance Computer Architecture (HPCA). , 2001, pp. 171-182.
[7] P. Chaparro, J. Gonzalez, G. Magklis, Q. Cai, and A. Gonzalez, “Understanding the Thermal Implications of Multi-Core Architectures,” IEEE Transactions on Parallel and Distributed Systems, vol. 18, pp. 1055-1065, 2007.
[8] V. Hanumaiah, S. Vrudhula, and K. S. Chatha, “Maximizing performance of thermally constrained multi-core processors by dynamic voltage and frequency control,” in IEEE/ACM International Conference on Computer-Aided Design – Digest of Technical Papers (ICCAD). , 2009, pp. 310-313.
[9] R. Rao, S. Vrudhula, and C. Chakrabarti, “Throughput of multi-core processors under thermal constraints,” in ACM/IEEE International Symposium on Low Power Electronics and Design (ISLPED). , 2007, pp. 201-206.
[10] C. Y. Cher and E. Kursun, “Exploring the Effects of On-Chip Thermal Variation on High-Performance Multicore Architectures,” Acm Transactions on Architecture and Code Optimization, vol. 8, Apr 2011.
[11] M. K. Cho, C. Kersey, M. P. Gupta, N. Sathe, S. Kumar, S. Yalamanchili, and S. Mukhopadhyay, “Power Multiplexing for Thermal Field Management in Many-Core Processors,” Ieee Transactions on Components Packaging and Manufacturing Technology, vol. 3, pp. 94-104, Jan 2013.
[12] M. P. Gupta, M. K. Cho, S. Mukhopadhyay, and S. Kumar, “Thermal Investigation Into Power Multiplexing for Homogeneous Many-Core Processors,” Journal of Heat Transfer-Transactions of the Asme, vol. 134, Jun 2012.
[13] P. Spalart and S. Allmaras, “A one-equation turbulence model for aerodynamic flows,” American Institute of Aeronautics and Astronautics, vol. Technical Report AIAA-92-0439 1992.
[14] S. V. Patankar, Numerical heat transfer and fluid flow / Suhas V. Patankar. Washington : New York :: Hemisphere Pub. Corp. ; McGraw-Hill, 1980.