Does a 10°C Increase in Temperature Really Reduce the Life of Electronics by Half?

This may seem like a silly question to ask in a magazine entitled “Electronics Cooling”, but why do we really care what temperature of electronics really is, anyway? The simple answer to that question is that it is universally recognized that electronics reliability when devices are too hot for too long of a time. The difficult answers to the question are in defining exactly what ‘too hot’ and ‘too long’ are. Since the objective of the field of electronics cooling is ultimately to ensure that electronics are reliable, it is worth thinking about the relationship between temperature and reliability.

If one were to ask people in the electronics industry how device temperature and reliability are related, it is likely that the most common response would be something along the lines of “the rule of thumb is that every 10°C increase in temperature reduces component life by half”. Using a common search engine, the search term “electronics reliability 10 degrees” yielded six references out of the first ten that mention that rule of thumb. Four of those references described how the rule is used while two described why it is incorrect.

The “10°C increase = half life” rule is based on applying the Arrhenius equation, which relates the rate of chemical reactions, R, to temperature, to failure mechanisms that occur in electronics. In applying the Arrhenius equation to electronics, it is assumed that the rate of chemical reaction corresponds to the damage to devices over time and the equation can then be used to compare the damage accumulated over time for different operating temperatures. The Arrhenius equation can be written as:

(1)

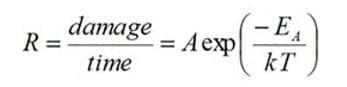
where A is a constant related to reaction, E_A is the activation energy associated with the reaction, k is the Boltzmann constant (8.617×10−5 eV/K) and T is the absolute temperature.

Equation (1) can be rearranged to develop an acceleration factor (AF) that relates the life of a component when it is operated at its use temperature, T_use to a test time at temperature T_test.

(2)

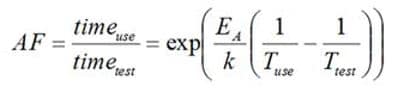
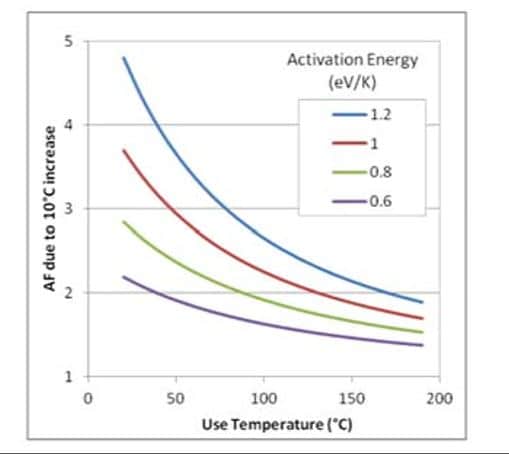
The activation energies for many different failure mechanisms in electronics have been reported in documents such as Ref.[1]. Many mechanisms have reported activation energies in the range of ~0.6-1eV/K. If T_test is set to 10K above T_use, Equation (2) can be used to estimate the acceleration factor as a function of T_use for different activation energies. For an activation energy of 0.8 eV/K over the temperature range of ~75-125°C, the resulting AF is ~2 – which leads to the “10°C increase = half life” rule of thumb.

This approach for using elevated temperature testing to estimate life time of electronics was popularized by MIL-HDBK-217, which was first published in 1965. The earliest reference that I have personally seen to a rule of thumb that relates a higher operating temperature to reducing operating life by half was in a proposal prepared by Collins Radio in 1968 [2]. Two interesting aspects of the information in that proposal were that a) ‘new’ results from MIL-HDBK-217 show that a 15°C increase in temperature reduces life by half and b) thermal cycling between minimum and maximum environmental temperatures decreased life by a factor of 8x. This suggest that from its birth it was recognized that the ‘10C=1/2’ rule of thumb was a rough approximation and factors other than operating temperature could very much affect electronics reliability.

The use of the Arrhenius equation in general, and the ‘10C=1/2’ rule in particular, has been criticized for the fact that it ignores significant failure modes that are not due simply to the maximum operating temperature [ 3, 4, 5]. Others have recognized the need to account for the multiple failure modes and have suggested statistical methods to define effective activation energies [6, 7]. The reliability of an electronics device is such a complicated issue that, even if the ‘10C=1/2’ rule is correct for a specific failure mechanism, it may be irrelevant for another. As an example, testing on a commercial resistive switching random access memory device found that it had an activation energy of 1.13 eV/K. With this activation energy, Equation (2) tells that the effect of increasing operating temperature from 45°C to 55°C would give an acceleration factor of more than 2; it would actually be ~3.8. However, using the researchers’ conclusion that the device could operate for 10 years at 85°C, this increase in temperature from 45 to 55°C would alter the predicted life from ~3800 years to ~1000 years. Presumably, other failure mechanisms would likely become relevant long before the maximum operating temperature would become of concern. In this case, to paraphrase Obi-Wan Kenobi, “These aren’t the failure mechanisms you’re looking for”.

In general, the Arrhenius model is likely appropriate for certain failure mechanisms including corrosion, electromigration and certain manufacturing defects [1], but is not suitable for other significant failure modes, such as the formation of conductive filaments, contact interface stress relaxation, and fatigue of packageto-board level interconnect [5]. Ref [9] reviews electronics failure modes that are influenced by temperature and discusses which of them can be modeled with the Arrhenius equation.

While it would be comforting to have a simple equation that can be used to quickly determine ‘how hot is too hot?’ in electronics, we live in a world that is a bit more complicated than that. Failing to recognize the severe constraints of the ‘10C=1/2’ rule of thumb can lead to problems. For example, many years ago a study showed that a heat pipe degraded over time, with the degradation following the Arrhenius equation. The author of that study then assumed that this result meant that the heat pipe followed the ‘10C=1/2’ rule and provided a reliability prediction guideline that propagated through a few publications. The original data provided sufficient data to estimate the activation energy and acceleration factors that significantly differed from the assumed rule of thumb [10].

While the Arrhenius-based reliability approach certainly has its limitations, when it is used correctly and its assumptions are understood it can provide reasonable predictions. An interesting, albeit dated, conference publication described how the reliability of avionics systems used in the F-15D aircraft changed when the F-15E, which provided 15°C cooler air to the electronics, was introduced. The mean time between failure (MTBF) for that fielded equipment improved with the lower temperatures by amounts equal to, or better than, the improvements predicted using MIL-HDBK-217 [10].

As many others before me have explained in detail, complex issues like predicting component reliability require complex approaches such as Physics of Failure to account for the combined effects. An overview of that analysis approach is beyond the scope of this article; the goal here was simply to point out that that the ‘10C=1/2’ rule, is really only valid for a failure mechanism with a specific combination of activation energy / operating temperature and only if that is the mechanism that leads to failure in a component.

REFERENCES

[1] William Vigrass, “Calculation of Semiconductor Failure Rates”, https://www.intersil.com/content/dam/Intersil/quality/rel/calculation_of_semiconductor_failure_rates.pdf (accessed July 2017)

[2] Ross Wilcoxon, “Advanced Cooling Techniques and Thermal Design Procedures for Airborne Electronic Equipment – Revisited” 2016 IMAPS Thermal Management Advanced Technology Workshop, Los Gatos, CA, October, 2016

[3] Patrick O’Connor, “Arrhenius and Electronics Reliability”, Quality and Reliability Engineering International, V. 5, N. 255, 1989, http://onlinelibrary.wiley.com/doi/10.1002/ qre.4680050402/pdf (accessed July 2017)

[4] Clemens Lasance, “Temperature and reliability in electronics systems – the missing link”, Electronics Cooling Magazine, November 1, 2001; https://electronics-cooling.com/2001/11/temperature-and-reliability-in-electronics-systems-the-missing-link/ (accessed July 2017)

[5] Michael Osterman , “We still have a headache with Arrhenius”, Electronics Cooling Magazine, February 2001; https:// www.electronics-cooling.com/2001/02/we-still-have-a-headache-with-arrhenius/ (accessed July 2017)

[6] Franck Bayle and Adamantios Mettas, “Temperature Acceleration Models in Reliability Predictions: Justification & Improvements”, “2010 Reliability and Maintainability Symposium,”; San Jose CA, USA; January 2010

[7] Mark Cooper, “Investigation of Arrhenius Acceleration Factor for Integrated Circuit Early Life Failure Region with Several Failure Mechanisms”, IEEE Trans. on Comp. and Pack. Tech., V. 28, N. 3, September 2005, pp. 561-563

[8] Jean Yang-Scharlotta , et al., “Reliability Characterization of a Commercial TaOX-based ReRAM”, Integrated Reliability Workshop Final Report (IIRW), 2014 IEEE International, South Lake Tahoe, CA, October 2014

[9] V.Lakshminarayanan and N.Sriraam, “The Effect of Temperature on the Reliability of Electronic Components”, Electronics, Computing and Communication Technologies (IEEE CONECCT), 2014 IEEE International Conference on; Bangalore, India; February 2014

[10] George Meyer and Ross Wilcoxon, “Heat Pipe Reliability Testing and Life Prediction”,2015 IMAPS Thermal Management Advanced Technology Workshop; Los Gatos, CA; October, 2015

[11] P.B. Hugge, “Field results demonstrate reliability gains through improved cooling”, Aerospace and Electronics Conference, 1994. NAECON 1994., Proceedings of the IEEE 1994 National; Dayton, OH; May 1994