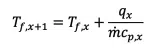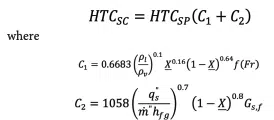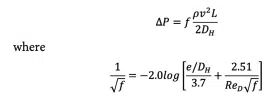Introduction
In the development of modern-day thermal management systems, we are continuously looking to implement coolants that offer high heat transfer performance, low pumping power requirements, are cost-effective and have a low environmental impact. Supercritical carbon dioxide (SCO2) has a range of incredible properties that lend it to meeting all these needs, even contending with conventional liquid-vapor phase change fluids that are actively cooling our high-demand electronic systems. The fluid does not experience critical heat flux conditions and has a relatively low operational temperature, at just over 31°C. Carbon dioxide is also a non-explosive, non-flammable, non-toxic fluid that is highly accessible and cost-effective. Admittedly, SCO2’s high operational pressure and heat rejection temperature requirements can pose design challenges that must be accounted for. However, SCO2 has already been integrated as an active fluid into a range of high-efficiency power cycles with promising results [1,2].
Characteristics of Supercritical Carbon Dioxide
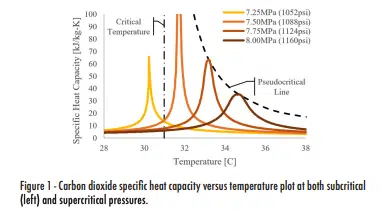
Carbon dioxide becomes supercritical when conditioned beyond critical point properties (31.1°C and 78.3 atm). At this state, the fluid experiences spikes in specific heat capacity that rival or exceed traditional phase change fluids, while operating at lower, gas-like densities. Figure 1 illustrates the specific heat magnitudes that can be achieved and the operational temperature envelopes that accompany them.
At subcritical pressures, specific heat capacity values spike at the saturation temperature, whereas at supercritical pressures they spike at the pseudocritical line. It is at this line – where the fluid transitions from a liquid-like to a gas-like state upon the absorption of heat –at which we want our systems to operate in order to maximize performance. Unlike the mechanisms behind conventional phase change, this process does not result in the generation of visible nucleation sites or bubbles. Instead, the fluid becomes less dense and consequentially easier to move. The combination of higher specific heat capacities and gas-like fluid density gives SCO2 the ability to effectively cool high heat flux components with lower pumping power requirements than many alternative phase-change systems.
This study is a direct continuation of the work performed by the Enhanced Heat Transfer Laboratory at Oregon State University (OSU) in 2019, where the first SCO2 cold plate made with additive manufacturing techniques was evaluated. The conclusions drawn from that study, in comparison to other industry-standard coolants, distinguished SCO2 as a highly competitive coolant for electronics cooling applications [3,4]. The experimental design of the present work aims to simulate a data center environment such that the results more closely reflect real-world applications.
Experimental Facility
A carbon dioxide conditioning loop, in conjunction with a heated experimental fixture, was constructed to generate and evaluate the performance of SCO2 in an electronics cooling application. The conditioning loop serves to pressurize and heat saturated CO2 (out of the cylinder) to the desired supercritical state. The heated experimental fixture is comprised of a pure copper block, surrounded by three inches of insulating Teflon™ and supplied with power by four cartridge heaters. A custom aluminum cold plate is bonded to an exposed copper surface that acts a hot processor chip surrogate.
The cold plate itself, which can be seen in Figure 2, was manufactured with direct metal laser melting techniques. Internally, it is comprised of seven parallel channels with hydraulic diameters of just over a millimeter and seven circular thru-holes, which are visible at the base. These holes are essential for the temperature-sensing technique utilized in this study. Geometric parameters and manufacturing tolerances of interest were verified using neutron radiography techniques at OSU’s TRIGA reactor.
While most of the sensing techniques used to capture data were fairly standard, one requiring further explanation is the fiber optic temperature sensor used to collect cold plate wall temperature values. By use of the phenomenon known as Optical Backscattering Reflectometry (OBR), this sensor is able to generate numerous, discrete temperature measurements along the length of a fiber optic cable. By routing this cable (back and forth) through the base of the cold plate, we are able to generate two-dimension al temperature maps that reflect the thermal performance of the coolant, as illustrated in Figure 3.
OBR utilizes Rayleigh backscattering techniques to pinpoint the location of the fiber optic cable relative to its Teflon sheathing. Light signal reflection times generate a baseline reading, and as the sheathing changes form under the application of heat and thermal expansion, the change in light reflection times may be correlated to changes in local strain and temperature. In our case, this allows for the collection of internal temperature measurements from within the cold plate wall and a deeper understanding of local heat effects at a frequency of 10 Hz [5].
Generating these temperature maps is essential to evaluating a given system’s local thermal management needs. Beyond the ability to visualize the streamwise temperature distribution of the cold plate itself, we are also able to see the exact location of localized hotspots and their magnitudes. Furthermore, these discrete wall temperatures can be used to compute local heat transfer coefficient values, which can be very powerful in evaluating performance and working towards system optimization. From this information, adjustments can be made such that the desired inlet fluid temperature and corresponding span are adjusted to provide the highest cooling capabilities to the regions of the heated surfaces that need it the most.
Evaluation of Performance
In conjunction with the experimental data captured, numerical models were generated for convective heat transfer coefficient (HTC) and cold plate pressure drop data sets. All of the data presented within this section were taken at a constant pressure of 7.93MPa (1150 psi), mass flow rate (500g/min), and input power delivered by the cartridge heaters (200W) – translating to a heat flux density of 41W/cm2 .
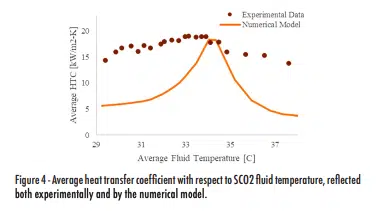
Figure 4 illustrates the relationship between the system’s average HTC and temperature. Here, it can be seen that maximum HTC values of around 19kW/m2 -K are measured at around 33.5°C – in close proximity to the expected pseudocritical temperature of 34.2°C. HTC values are also generally higher when the fluid is at lower temperatures (liquid-like) and begin to drop off as the fluid becomes increasingly gas-like. While there is an apparent disconnect between the numerical model and experimental data, it should be noted that the model captures the general trends of the experimental data – and even reflects comparable HTC values around the pseudocritical temperature, which would likely be the target operational point set by designers.
Experimental HTC values were computed using Newton’s Law of Cooling, assuming a uniform heat flux. Local wall temperatures are reflected by the OBR temperature measurements, while the fluid temperature was computed using calibrated thermocouples in the flow stream at the cold plate’s inlet and outlet. The heat transfer area used in this calculation reflect the area of the channels themselves (with the exception of the top surface).
While all of the local wall temperatures could be directly measured through the fiber optic sensor, only the inlet and outlet fluid temperatures were experimentally measured. An energy balance on the fluid was utilized to compute average local fluid temperature values from within the cold plate, with the outlet temperature bounded by the experimental reading.
Numerically modelled HTC values were computed by use of a flow boiling correlation, which was adapted for supercritical fluid use by altering the thermodynamic quality and saturation properties accordingly [6]. Here, the single-phase HTC values were computed using the Dittus-Boelter equation. The supercritical HTC values (SC) were computed by multiplying the computed single-phase HTC (SP) by two constants – which incorporate a ratio of the fluid densities at effective “supercritical” saturation temperatures, a supercritical quality and a specific enthalpy term with the Froude number assumed to be unity as well as the surface–fluid combination value (Gs,f).
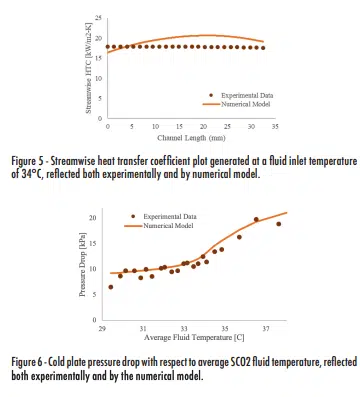
Figure 5 shows how the local HTC varies in the streamwise direction of the cold plate, also using the above equations. Here it can be seen that the experimentally generated HTC values experience very little change, whereas the numerical model predicts more variation. This is likely due to the uniform heat flux assumption that had to be made without the implementation of a thermal test vehicle (TTV). Nonetheless, the streamwise model again comes close to predicting HTC values near the pseudocritical temperature. Knowledge of the local heat flux distribution would likely close this gap and give more merit to the numerical model.
Figure 6 demonstrates the relationship between cold plate pressure drop and average fluid temperature. As the fluid heats up, the Reynolds number increases due to thermodynamic fluid property changes, driving up friction factor values and therefore pressure drop values. The inflection point, again near the pseudocritical temperature, is indicative of favorable operational temperatures.
Experimental values were collected by use of a high-accuracy differential pressure sensor and modeled values were generated through the Darcy-Weisbach equation in conjunction with the Colebrook equation.
Temperature sweeps were conducted to evaluate optimal SCO2 operational temperatures for the given fluid pressure. From the data presented, an operational temperature range of around 33- 34°C produced the highest HTCs with reasonably small pressure drops and therefore lower pumping power requirements.
Conclusions
When pressurized to 7.93MPa (1150psi) and flowing at only 500g/min (1SLPM), SCO2 was able to produce HTCs nearing 20kW/m2 -K, dissipating heat flux densities of 41W/cm2 within a relatively simple cold plate that had just seven parallel channels and exhibited no sign of a critical heat flux condition. At the same operational parameters, a pressure drop of only 12kPa was measured; requiring only 0.1% of the input power to pump the fluid through the cold plate. In conjunction with SCO2’s low environmental impact and abundance, this study is indicative of the fluid’s potential as a highly competitive coolant in electronics cooling applications. It is also important to mention that operation at pressures nearer to the critical point and geometric optimization could substantially improve upon the metrics displayed here. It is expected that the numerical models generated for this study, while able to produce experimentally comparable values, would have a better agreement if the local heat flux density was known, thereby warranting future studies.
References
[1] Weiland, N. T., R. A. Dennis, S. Lawson, and P. Strakey. 2017. Fundamentals and applications of supercritical carbon dioxide (sCO2) based power cycles. (K. Brun, P. Friedman, and R. Dennis, eds.). Oxford Woodhead Publishing.
[2] Marion, J. 2022. “Supercritical CO2 10 MW Demonstration Project Under Construction.” Turbomachinery International, 2022.
[3] A. Nordlund, M. Harrison, B. Fronk, J. Gess, 2019, “Operation of a Supercritical CO2 Cold Plate for Electronics Cooling Applications” Thermal Technologies Workshop, Redmond WA
[4] B. Ramakrishnan et al., “CPU Overclocking: A Performance Assessment of Air, Cold Plates, and Two-Phase Immersion Cooling,” in IEEE Transactions on Components, Packaging and Manufacturing Technology, vol. 11, no. 10, pp. 1703-1715, Oct. 2021, doi: 10.1109/TCPMT.2021.3106026.
[5] Optical Backscatter Reflectometry (OBR) Overview and Applications Introduction Reflectance and Return Loss Measuring Return Loss. n.d. Accessed: May. 17, 2023, https://www.lunainc.com/sites/default/files/assets/files/resource-library/OBR%20-%20Overview%20and%20Applications.pdf
[6] Kandlikar, S. G., J, Heat Transfer, 112, 219, 1990.