One of the “fairy tales” that I see as a trend in thermal engineers performing electronics cooling is that they become dependent on the capabilities and methodology of the particular software they use. If the help guide or our mentor showed us how to solve a particular problem with our software tool and it worked, we may not have a reason to change even if the method is not the most efficient one. Frequently, we learned some math in school, but do not take advantage of all the tools and techniques our teachers required and encouraged us to master. The topic for this column is superposition with transient information and the fact is that the application of superposition can be very beneficial in assessing time dependent information. As a general topic, superposition has been mentioned in Electronics Cooling a few times [1], but not specifically in this manner.
It is helpful to remind readers that the principle of superposition is applicable only for linear systems. In the electronics cooling field, this usually means that the thermal properties may be assumed constant, radiation effects are minimal, and convection may be represented in a linear fashion (such as a constant heat transfer coefficient back to a constant reference temperature). While there are always exceptions, many of the problems we solve are reasonably well represented by a linear model.
Assessing the dynamic thermal response of electronics systems is a reasonable expectation from a thermal design engineer. Two of the most common questions regarding the transient thermal response of electronics system that I have been asked are:
1. How long does it take to heat up and, related, how long to cool down?
2. What happens if the electronics are turned on and off?
The use of superposition in the time domain is a very useful tool to answer these types of questions and is briefly illustrated by the following example.
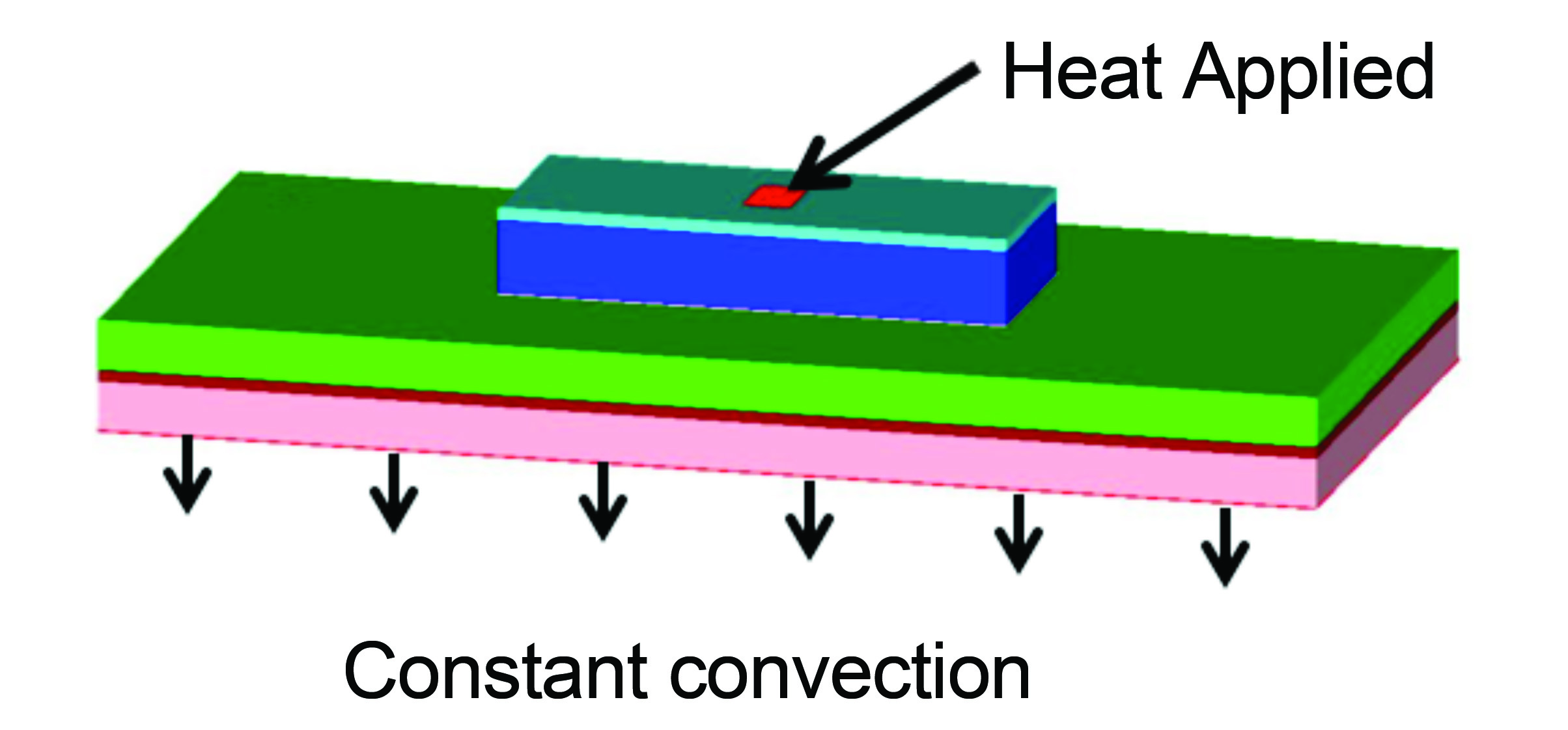
Consider a simple thermal system illustrated in Figure 1. The system consists of a few different materials and interfaces and a constant convective boundary condition on the lower surface to a constant reference temperature with all of the other surfaces assumed adiabatic. For the purposes of this column, a numerical model was created with the thermal properties and heat load adjusted such that the temperature response to a step change in the heat value and measured at the center of the heated area results in the time-temperature curve shown in Figure 2a and 2b. The initial temperature was set to a uniform value and both the initial temperature and the reference temperature were set to zero to simplify the use of superposition. Note that the system has an initial rate of temperature increase (in the first unit of time) that is rapid compared to the rate of temperature increase at later times. By about 15 time units, the system has achieved steady-state.
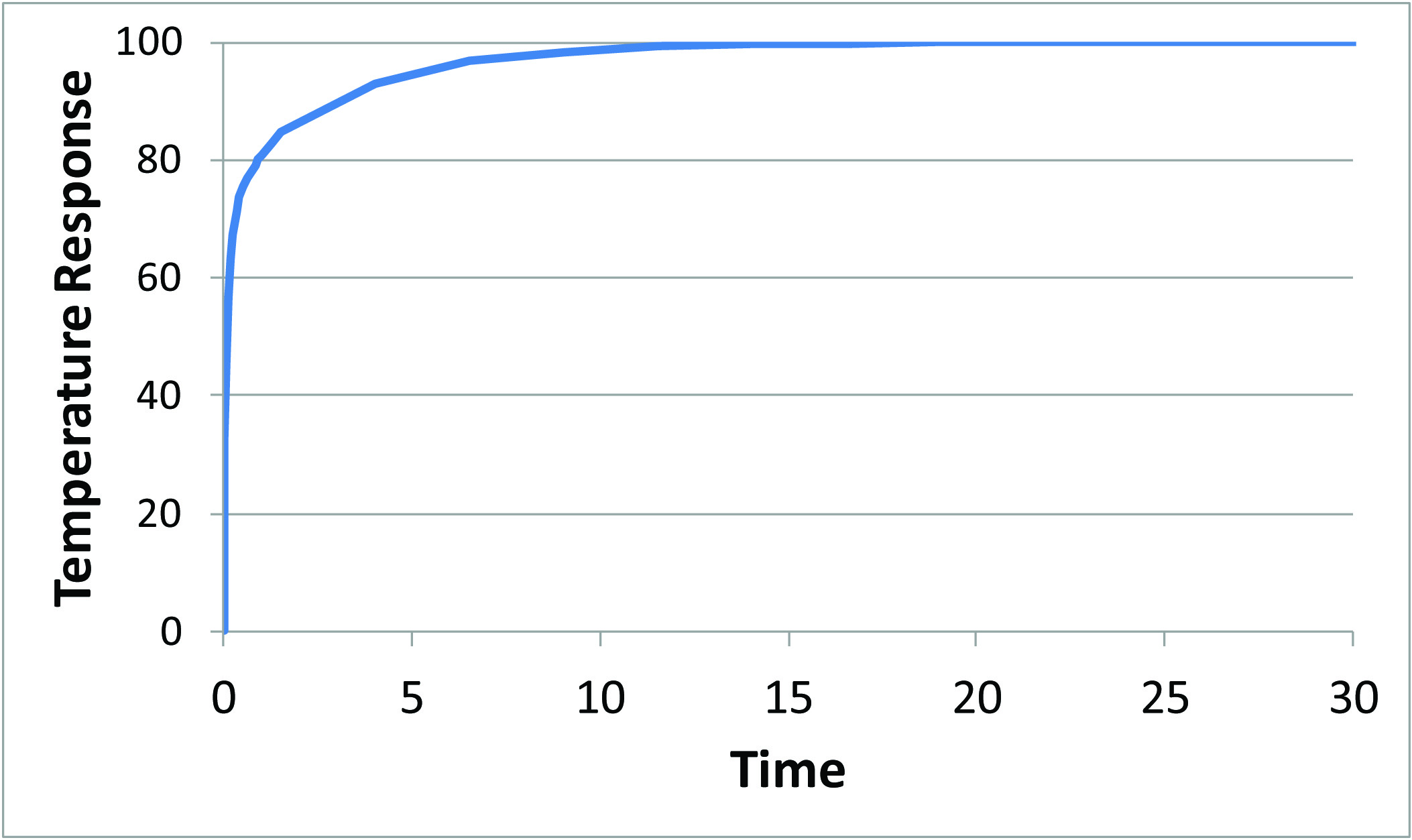
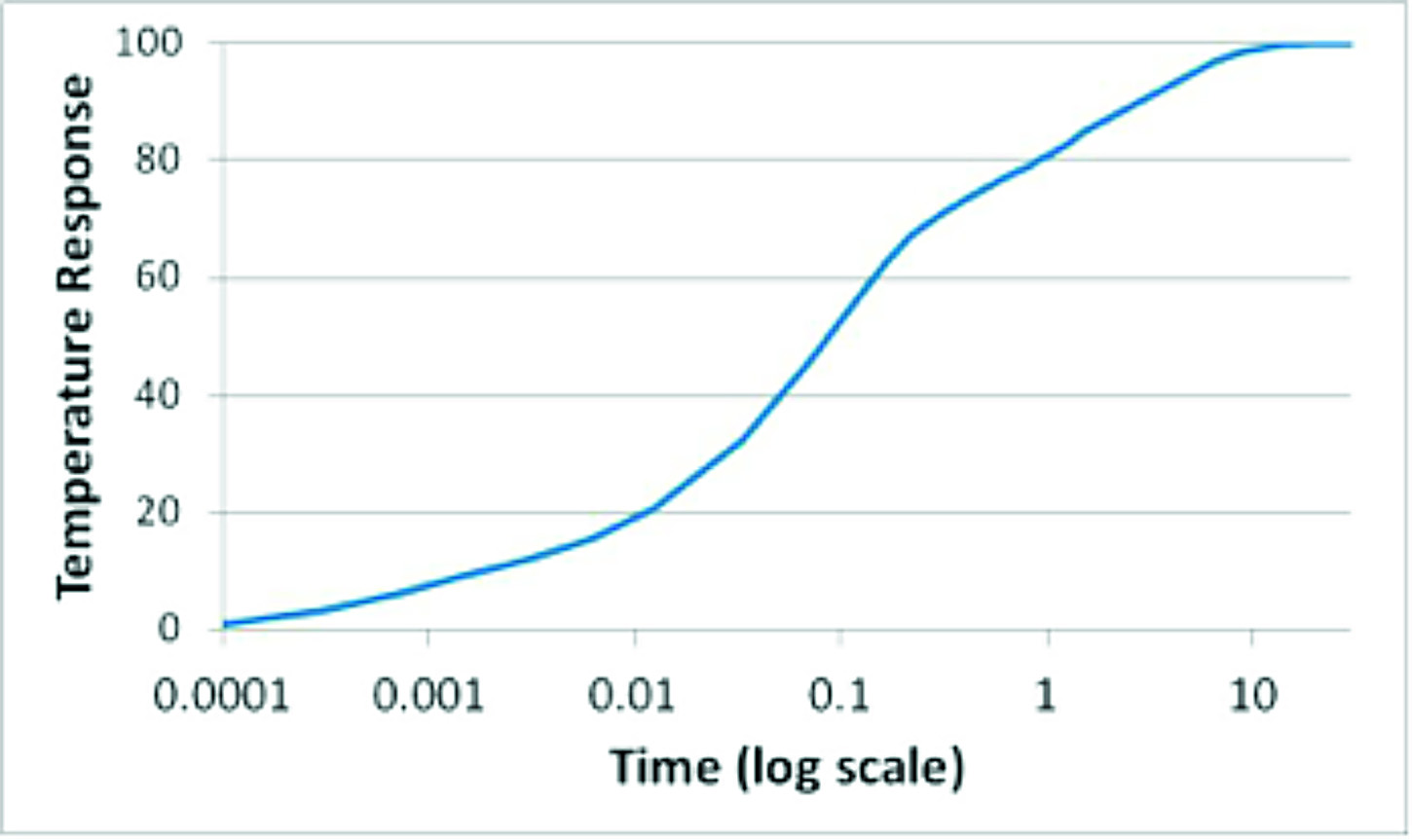
Figure 2a and 2b both contain the same information, but plotted on both a linear and logarithmic time scale. The advantage of plotting the response on a log scale for time (2b) is that the different materials and interfaces may be seen. Assuming that the response is accurate in time and space, this response represents a time history of the heated region to a step change in power. Since the system is linear, if only one-half of the heat load was applied, the time dependent curve could be scaled by a factor of 0.5 such that it would have reached a value of 50 at steady-state.
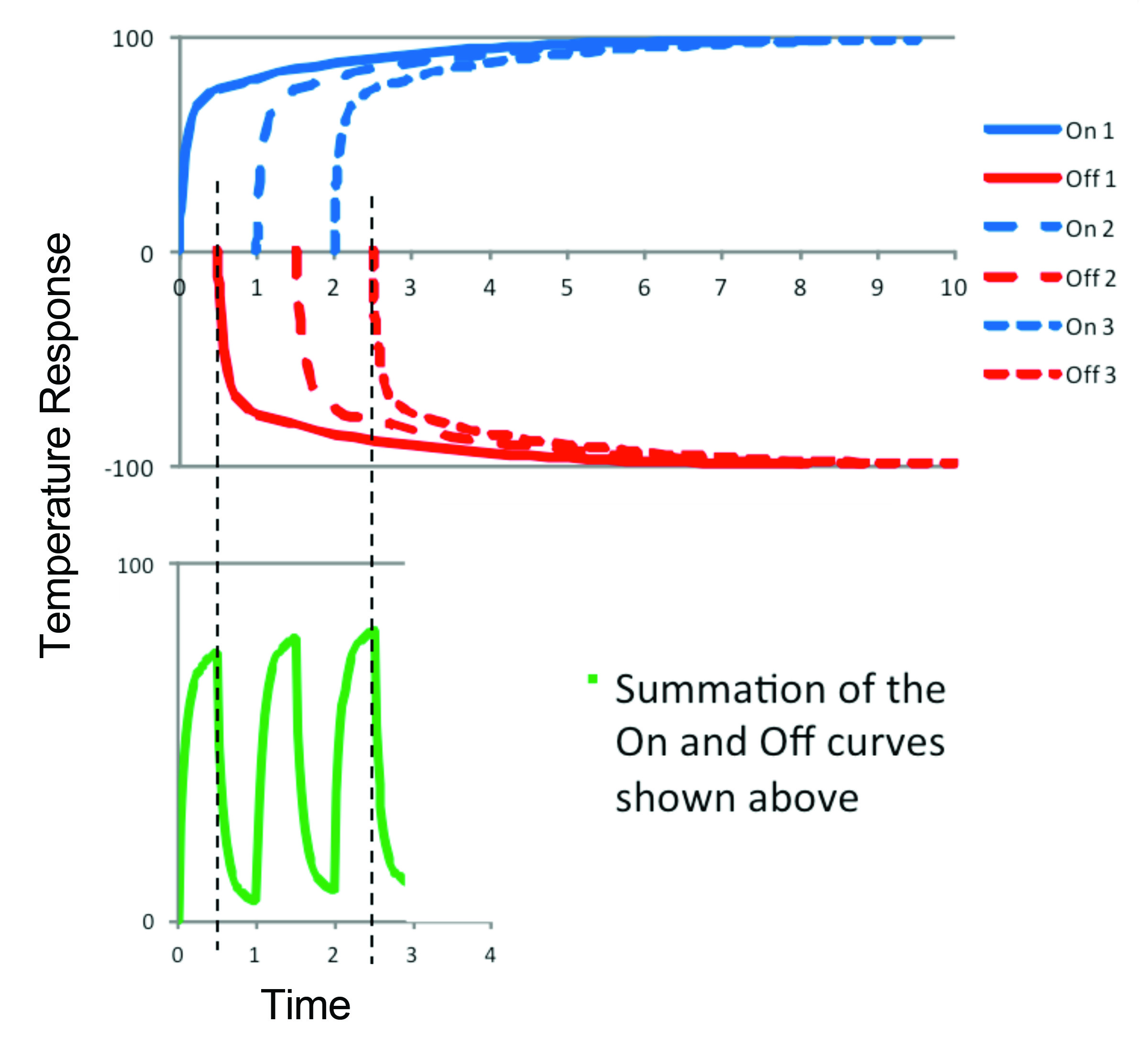
While this was probably obvious to most readers, using this same information and superposition allows a prediction of the response to turning the power on and off to be made. As an example, suppose that the power was on for 0.5 units of time and off for 0.5 units of time and that this cycle repeated. Using the transient response in Figure 2, a periodic curve may be generated as the superposition of on and off responses. This is shown graphically in Figure 3. The on and off curves are time shifted so that the start of the curve coincides with the start of a powered or off-state response. The response temperature is the summation of the time history of the responses that have occurred at a particular time value. For example, the response between 1 and 1.5 units of time is the summation of On 1, Off 1, and On 2.
As a check, the same simple model described in Figure 1 was modified to have the heat applied with the time profile (0.5 time units on and 0.5 time units off) and a comparison between the results is shown in Figure 4. The small difference between the two curves is a result of grid convergence in time, which brings up an additional benefit of superposition. It is often easier to do a time-step convergence study on a step-change response than it is on a cyclical power application case because of the need for small time steps where the system responds to an on or off application of the heat load.
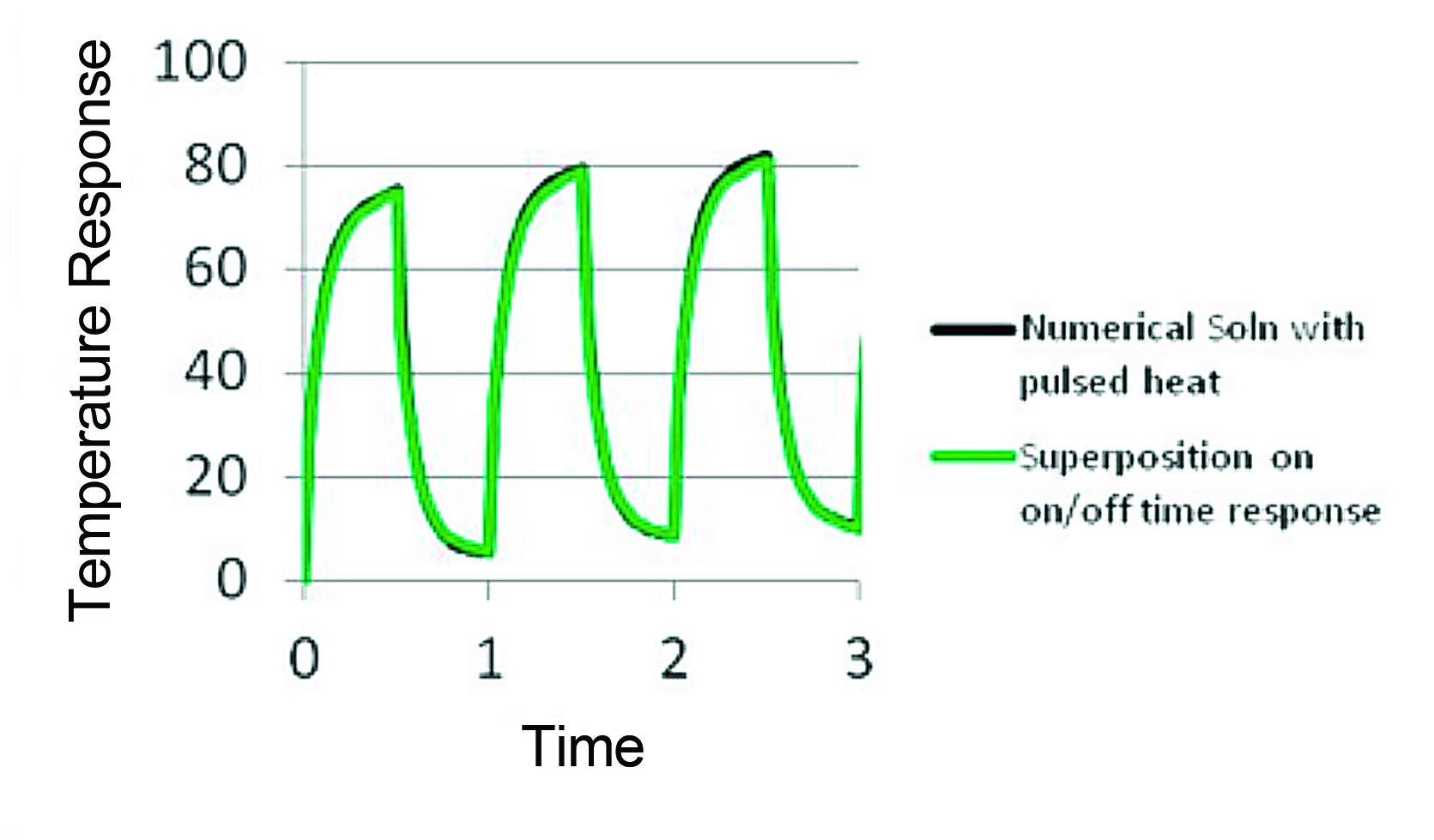
A useful feature of this technique is that it is easy to generate the temperature response to different combinations of on and off cases and even different heat loads.
Note that the curve represented in Figure 2 did not necessarily need to be generated by a thermal model. The response could have been measured test data. Provided that the test data were a response to a step change in heat load and the system could be considered linear, the same superposition process would apply. A caution is in order using this technique, especially in systems with a large variation in time scales (such as features on an IC requiring time scales on the order of μsec coupled with other parts of the system that respond much slower such as seconds or minutes). In order to accurately use superposition, a complete time history curve to steady-state is required, and then care is required in the area of numerical precision because the response out at the later times is the summation of many preceding responses.
References
[1] Guenin, B, “Power Map Calculations Using Image Sources and Superposition”, ElectronicsCooling, Nov, 2008.






