Convection air cooling is still the most commonly used method of coolingmicroelectronics. In order to deliver air cooled computer equipment with higherreliability, we need to focus on the life expectancy of the air moving devices(AMDs). However, this is not a trivial exercise because there are so manyvariables and there is no industry standard for AMD life test procedures. Therefore, it may not be meaningful to compare life expectancy information fromdifferent AMD vendors. We have first to understand the vendor’s fan failuredefinition and then to consider life test procedure, and the fan life expectancycalculations. The purpose of this article is to explain these topics and toencourage the standardization of fan life evaluation, as outlined in [1].
Definition of Fan Failure
Fans may fail in several ways and failure may be defined differentlydepending upon the applications. Fan failures typically include excessivevibration, noise, rubbing or hitting of the propeller, reduction in rotationalspeed, locked rotor, failure to start, etc.. Table 1 lists the failure criteriathat different vendors are using in their AMD life tests.
| Vendor A | Vendor B | Vendor C | Vendor D | Vendor E | |
| Rotational Speed, N | < 0.9 N initial | < 0.8 N nominal | < 0.9 N initial | 0 rpm | < 0.7 N initial |
| Running Current, I | < I maximum | < 1.2 I nominal | N/A | N/A | N/A |
| Acoustic Nose | + 3dBA | N/A | +3 dBA | + 5 dBA | N/A |
Table 1. Failure criteria
It is worth mentioning that no AMD stops moving air because of increasednoise. The increased noise is a result of a bearing failure and the bearingfailure is usually caused by the loss of lubricant, which leads to wear in thebearing.
In addition, the capacitor may fail in AC AMDs and the electronics maycontribute to early failures in DC AMDs. Failure criteria in life tests can alsoinclude a change in coast-down time or start time to reach full speed. Problemswith coil insulation breakdown or failures of that type can be classified asworkmanship problems or an out-of-control manufacturing process.
Reliability Concepts
Fan reliability can be measured in several ways. The data for a life test,can be plotted as a cumulative distribution which shows the total fraction offans failing up to any operating time. A sample cumulative distribution isplotted in Fig. 1 for a vendor’s test which was stopped at 8,400 hours after 18out of 48 fans had failed [1].
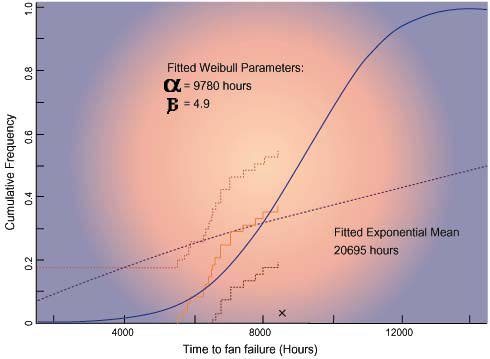
A few AMD vendors provide prospective customers with reliability informationbased on the exponential assumption. However, life test data, such as shown inFig. 1, does not support the use of the exponential distribution. Pastexperimentation and model fitting has shown that the Weibull distributionprovides a good fit to fan life data, because it accurately represents wear-outphenomena. Therefore, the use of the exponential distribution is misleading,because it distorts the data and ignores the wear-out of the AMDs.
For the Weibull distribution, the cumulative distribution
function (CDF), a function of age t, is given by [2]
F(t)=1-e-(t/)ß[1]
where is thecharacteristic life and ß is the shape parameter. Shape parameters forWeibull models fit to fan life are generally greater than 1, which means that afan’s failure tendency increases with age (wear-out). The reliability functionequals 1 – F, which at any age t represents the proportion ofsurvivors from the original population. The Weibull hazard rate (also known asthe failure rate or hazard function) is given by
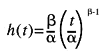
Two metrics of fan reliability commonly quoted by vendors are the L2life and L10 life, which are the second and tenthpercentiles under some assumed fan life distribution such as the Weibull. SinceF(t) = 0.1 at L10 and 0.02 at L2 inequation (1), we get:
L10 = (0.10536)1/ß
L2 =
(0.02020)1/ß
[3]
For example, given =100KPOH and ß=1.5, L2=7, 418 hours represents the age at which98% of the population is expected to still be operating. The advantage ofspecifying an L2 life in place of L10 life is that thedesired early life failure distribution is more tightly specified.
Sometimes vendors will also quote the Mean Time To Failure (MTTF). For theWeibull distribution,
MTTF = (1+1/ß) [4]
where denotes theGamma function.
It is worth mentioning that the MTTF is often confused with the Mean TimeBetween Failures (MTBF). The MTBF should only be used in a repairable systemssetting. If a machine has ten fans in it, and any failed fan is promptlyreplaced, then the MTBF may be used to understand the system’s maintenance needsand service cost. But since the underlying hazard rate of the fans is notconstant, computing the MTBF of a multiple-fan system is quite difficult. Instead, system reliability issues often are settled by inputting a one-numberhazard rate for the individual fans, in which case the average hazard rate maybe appropriate [1].
Fan Life Estimation
The life of most fans is limited by the bearings. Electronics, even in DCfans, play a secondary role. Bearing life is generally limited by the greaselife, which is primarily a function of temperature. Grease life is affected bythe type of grease, percentage of grease fill, operating environment, load, andbearing design. The Booser grease life equation is based on grease life testson electric motor bearings, but it holds true for any rolling-element bearing. The equation for the bearing grease life in the application is [3]
logL10=-2.6 +(Kt/Tbrg)-0.301S [5]
where
S=SG+SN+SP
SN=0.86DN/(DN)L
SP=0.61DNP/C2r
| P | Equivalent Dynamic Bearing Load, lbf |
| N | Speed, rpm |
| Cr | Basic Dynamic Load Capacity, lbf |
| D | Bore Diameter, mm |
| (DN)L | Speed Limit, rpm-mm |
| S | Half-life Subtraction Factor; for S = 1, the life drops 50% |
| SG | Grease Half-life Subtraction Factor, typically 0 for many greases |
| SN | Speed Half-life Subtraction Factor |
| SP | Load Half-life Subtraction Factor |
| KT | Grease Temperature Factor = 2450 for acceleration factor of 1.5 for each 10°C |
| Tbrg | Bearing temperature, K |
This equation, however, does not account for the effect of grease quantityand may not cover all greases on the market, particularly modern greases whichuse synthetic oils. For these new greases and depending upon the operatingconditions, the results from the Booser equation may be conservative. Therefore,unless adjustment factors are available for a certain fan type, it is best touse the Booser equation to obtain a qualitative comparison of two fan designsrather than an absolute life estimate.
Example 1 The following information was obtained from a fan vendor.
P = 960 g (2.116 lb), Cr = 57 Kg (125.66 lb),
D = 3 mm
N = 2200 rpm, (DN)L = 270,000 rpm-mm,
Tbrg = 42°Cwhen Tamb = 25°C
The half life subtraction factor is calculated as
S = SG + SN + SP= 0 + 0.021 + 0.540 = 0.561,
and the resulting life estimate is
L10 = 102,000 hours.
In situations where fan reliability is critical, it is a good idea to limitthe bearing temperature rise to 10°C. This rule of thumb should generallybe applied when a single fan failure results in a system shut-down.
The Booser life estimate can also be significantly affected by the bearingload and the bearing size. Installing a fan with the shaft mounted verticallywill result in a lower bearing load and a longer fan life. Using a largerbearing will also yield a longer fan life.
In addition to grease life, bearing load rating life is a long establishedmethod of estimating bearing life based primarily on bearing loads and capacity. International standard ISO 281 [4] and bearing catalogs describe the method. It typically yields life values longer than most fan vendors will support. Manybearing vendors have devised adjustment factors for parameters other thanbearing load. For information on a specific fan, consult with the fan vendorand bearing supplier.
Fan Life Experiments
On account of economic and time constraints, we may rely on a zero failuretest strategy and/or accelerated testing techniques. A zero failure teststrategy may be used to estimate the test time required to verify a lifeexpectancy criterion such as a minimum L10 life. Note thatthe precision of this approach depends on the accuracy of the shape parameterassumption [5].
Example 2 How long should a sample size of 30 fans be tested todetermine with 90% confidence that L10 is greater than orequal to 80,000 hours, at 30°C? Based on Breyfogle [5, equation (12.7)]and assuming a Weibull distribution, each of n fans should be testedt1 hours, with
t1 = [
22;C /2n] 1/ß
where 22 is the C-th percentile of the Chi Square distribution with two degrees offreedom; C is determined by the desired confidence level. From a Chi Squaretable, we get
22;0.90 = 4.60
Assuming ß = 2, we solve for a in equation (3) to obtain
= L10(0.10536)-1/2= 246,463 hours
Now substitute intoequation (6), with n = 30 to get t1 = 68,280 hoursof test time for each fan. If all 30 fans operate t1 hours(at 30°C), without failure, then we will be able to assert with 90%confidence that L10 is at least 80,000 hours.
Accelerated Life Testing
The previous example shows that life test durations are very long, even whena zero failure test strategy is used. Therefore, accelerated testing techniquesare essential to complete component evaluation within a reasonable time andcost.
Care must be taken when selecting an accelerated test strategy. Anacceleration model that does not closely represent the characteristics of an AMDcan result in an invalid conclusion.
The first acceleration factor shown in Table 2 is on/off cycles. Thesecycles stress the AMD by accelerating the bearing from zero speed to normalspeed. An on/off cycle every 8 hours would be representative of a personalcomputer application. Even if this degree of stress is not appropriate, someon/off cycles are required to detect AMD problems such as failure to start,changes in rotational speed, coast down time or start time, and increased noise.
An example of the problem of not identifying fan failures is provided byTables 1 and 2. Table 2 indicates that some vendors do not use on/off cycles toidentify failures and Table 1 shows that for Vendor E, reduced rotational speedis not considered a failure until it has dropped 30%, a very loose failurecriterion. It should be expected that Vendor E, using this combined testdefinition, will report AMD life values that are much higher than normal.
| Vendor A | Vendor B | Vendor C | Vendor D | Vendor E | |
| On/Off Cycles | Every 500 hours | None | Biweekly (336 hours) | None | None |
| Air Temp. During Life Tests | 80±5°C | 75°C | 72°C | 70°C | 85°C |
| Temperature Acceleration Factor | 2.0/10°C | 1.482/10°C | 2.0/10°C | 1.315/10°C | 2.0/15°C |
Table 2. Acceleration Factors
Elevated temperature is generally the primary acceleration factor. The rangeof acceleration factors typically used in AMD reliability calculations is shownin Table 2. For AMD failures caused by lubricant breakdown, it is reasonable touse the acceleration factor of 1.5 per 10°C as in Booser’s equation. Forexample, to extrapolate the results of a life test run at 80°C down to 40°C,use an acceleration factor of 1.5(80-40)/10 = 5.1.
What is the upper temperature bound for accelerated AMD life testing? Atthe accelerated life test temperature, there should not be a significant changein grease structure. The performance of the grease is degraded mainly due toevaporation loss and oxidation. Based on the ASTM standard test methods forevaporation loss and oxidation characteristics of lubricating greases and oils,accelerated life testing should be conducted at temperatures below 90°C[1].
What is the minimum ambient temperature to which fan life test data may beextrapolated using the temperature acceleration factors given in Table 2? Booser’s nominal temperature acceleration factor applies specifically at abearing temperature of 100°C.
Therefore, applying these acceleration factors down to a room temperature of25°C is probably questionable, but that is often how they are used becausea better model is not available.
Conclusion
As different companies use different approaches, it is useless to comparethe life expectancy information from one vendor with that from other vendors. Thermal Engineers and Component Evaluation Engineers have to perform anindependent comparative analysis when selecting an AMD. Parameters of importancein fan life analysis include failure criteria, the distribution functions forstatistical analysis and the life test acceleration factors. Once theseparameters are selected, they should be used consistently in order to comparedifferent AMDs. We hope the material presented here will help encouragestandardization in fan life evaluation.
Sung J. Kim
IBM Storage Systems Division,
9000 S. Rita Road,Tucson, Arizona 85744, USA
Tel: +1 520-799-2120 Fax: +1 520-799-4788
Email:sung@vnet.ibm.com
Alan Claassen
IBM Storage Systems Division,
5600 CottleRoad, San Jose, California 95193, USA
Tel: +l 408-256-6288 Fax: +l408-256-2095
Email:aclaassen@vnet.ibm.com
References
1. Kim S., Vallarino C. and Claassen A., 1996, “Reviewof Fan Life Evaluation Procedures,” International Journal of Reliability,Quality, and Safety Engineering (in press).
2. Tummala R.R., and Rymaszewski E.J., 1989, Microelectronics PackagingHandbook, Van Nostrand Reinhold, New York, Chapter 5.
3. Booser E.R., 1974, “Grease Life Forecast for Ball Bearings”, Lubrication Engineering, pp. 536-541.
4. International Standard ISO 281, 1990, “Rolling Bearings – DynamicLoad Ratings and Rating Life”.
5. Breyfogle III, F.W., 1992, Statistical Methods for Testing, Development,and Manufacturing, John Wiley and Sons, New York.






