When a designer has to deal with thin current-carrying wires, a number of thermal issues pop up: Joule heating, heat losses and temperature measurement. For standard lead wires, one usually wants minimal Joule heating and minimum thermal resistance (in order to maximize the heat losses). Minimization of heat losses may be important for a research environment. Maximum Joule heating is required for heaters, and their resistance is a good measure for the average temperature. In this case one wants to maximize the temperature coefficient, α, of the metal.
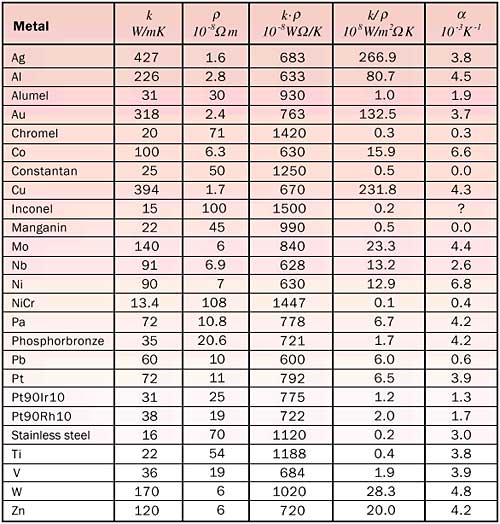
In all cases it is helpful to compare the electrical and thermal properties of the wires. As is well known (see, for example, Technical Data, ElectronicsCooling, May 2000, Vol.6, No.2), electrical and thermal properties are linked through the Wiedemann-Franz law, which states that the ratio of the thermal conductivity k and the electrical resistivity r is more or less constant for a given temperature. As is apparent from Table 1, this ‘law’ cannot be used for design purposes. Indeed, large deviations are possible, up to a factor of three.
Following are the design equations.
The heat transfer via conduction through the wires is determined by:
with L the length of the wire and r its radius.
For the Joule heating of the wires we have:
Let us consider two cases.
The first case concerns the ‘standard’ use of wires; for example, to connect a package to a board. For minimum thermal resistance L should be minimal and k and r maximal. For minimal Joule heating ρ and L should be minimal and r maximal. This means that in this case there is no problem with the dimensions, and we need to maximize the ratio k/ρ.
The second case concerns a lab experiment in which we want to limit the heat losses, for which the wire thermal resistance should be maximized and Joule heating minimized. In this case the requirements for L and r are contradictory. This means that the only option is to minimize the product of k times ρ. Finally, if we would like to use the electrical resistance of the wire as a temperature metric, we need the temperature coefficient of resistivity, and the higher the better.
Table 1 contains values for the thermal conductivity, the electrical resistivity, the product k� ρ , the ratio k/ρ , and the temperature coefficient. (Note that the data are given at room temperature.) Of course, one should realize that other requirements must be taken into consideration for the final choice. For example, weldability or solderability may be important design parameters.
Table 1. Various Data at Room Temperature
 |
A final remark: If one properly chooses the wire dimensions and properties, it is possible to reduce to zero the heat losses through conduction via the wires by letting Joule heating compensate for the heat losses.




