The Technical Data column of the previous issue discussed the concept of thermal diffusivity. It makes sense to discuss in this issue a related topic: thermal effusivity. While thermal diffusivity, a, is defined as the ratio between the thermal conductivity, k, and the volumetric thermal capacity, ρcp, the effusivity, e, is related to their product, as follows:
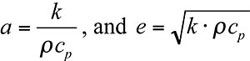 |
It is important to realize that while the two expressions contain the same parameters, they are quite different. Diffusivity is related to the speed at which thermal equilibrium can be reached. Effusivity (sometimes called the heat penetration coefficient) is the rate at which a material can absorb heat. It is the property that determines the contact temperature of two bodies that touch each other.
For example, it explains the well-known but often misinterpreted effect that a metal feels cold to the touch and wool warm, even when both are at room temperature. Our finger is a very poor temperature sensor (that is, of the temperature of the body it touches, not of the contact temperature), but a sensitive heat flux sensor. The contact temperature is lowest for materials with a high thermal conductivity and a high thermal capacity, explaining why metal feels cold.
While the thermal diffusivity a is only related to time-dependent heat transfer, the contact temperature is time-invariant as long as the two materials may be considered infinite. When is such the case? This is ‘controlled’ by the thermal penetration depth δ, roughly equal to 2√(a�t), with t the time. It is essentially the distance from the surface at which the temperature begins to rise at some time t after excitation at the surface.
In a number of industrial applications it is the effusivity that is the controlling parameter, not the diffusivity. One example is injection molding, whereby the contact temperature between the wall and the hot plastic determines the required pressure (due to solidification at the wall) and the cycle time. The best solution is to coat the wall with a thin layer of low conductivity material, thereby raising the contact temperature during injection while hardly influencing the cooling time. Another example can be found in the pharmaceutical industry where measuring the effusivity of pills, for example, is an established quality criterion.
Because, for most solids, the thermal capacities lie in a rather narrow range (see the Technical Data column of May 2003), it might be concluded that, to a first order, the diffusivity scales with k and the effusivity with √k. From this perspective, both quantities are related, which becomes obvious from looking at Figure 1, where only the solids from Table 1 are included. The two outliers are the ones with a relatively low density.
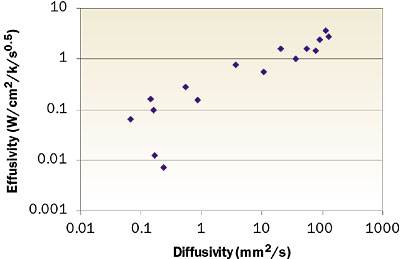 |
Figure 1. Thermal effusivity vs. diffusivity for the solids presented in Table 1.
It is interesting to understand how a and e are measured. As discussed previously, the diffusivity determines how fast some point away from the temperature excitation is heated, while the effusivity is related to a temperature at the surface. Measuring both quantities provides the thermal conductivity without the need to know the thermal capacity. Many methods are described in the open literature, based on either contact techniques or photo -thermal methods where a modulated heat source generates temperature excursions of which the amplitude and phase can be used to extract both a and e at the same time.
Table 1 shows data for a number of typical materials. Also presented is the penetration depth, calculated 1s after excitation. Please note the units.
Table 1. Thermal effusivity (from low to high) for selected materials at room temperature. The penetration depth δ is tabulated at 1s after excitation.
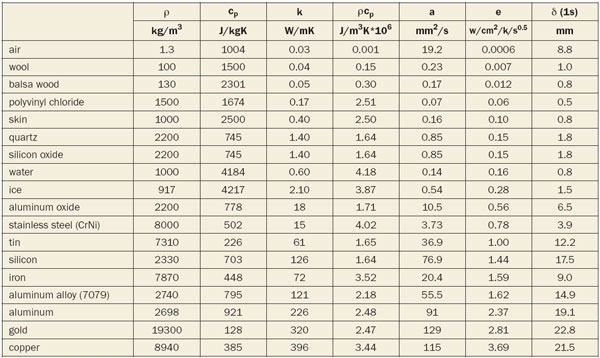 |





